题目内容
9. 某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况.如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )
某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况.如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )| A. | 300米 | B. | 150$\sqrt{2}$米 | C. | 900米 | D. | (300$\sqrt{3}$+300)米 |
分析 由题意可得在Rt△ACD中,∠A=30°,CD=300米,在Rt△BCD中,∠B=45°,然后利用三角函数,求得AD与BD的长,继而求得答案.
解答 解:∵在Rt△ACD中,∠A=30°,CD=300米,
∴AD=$\frac{CD}{tan30°}$=$\frac{300}{\frac{\sqrt{3}}{3}}$=300$\sqrt{3}$(米),
∵在Rt△BCD中,∠B=45°,CD=300米,
∴BD=CD=300米,
∴AB=AD+BD=(300$\sqrt{3}$+300)米.
故选D.
点评 此题考查了俯角的定义.注意能借助俯角构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
19.下列命题:
①一组对边平行,另一组对边相等的四边形是平行四边形;
②对角线互相平分的四边形是平行四边形;
③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD是平行四边形;
④一组对边平行,一组对角相等的四边形是平行四边形.
其中正确命题的个数是( )
①一组对边平行,另一组对边相等的四边形是平行四边形;
②对角线互相平分的四边形是平行四边形;
③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD是平行四边形;
④一组对边平行,一组对角相等的四边形是平行四边形.
其中正确命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.若-2an-1-4an+1的公因式是M,则M等于( )
| A. | 2an-1 | B. | -2an | C. | -2an-1 | D. | -2an+1 |
18.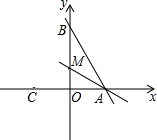 如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
 如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )| A. | (0,4) | B. | (0,3) | C. | (-4,0) | D. | (0,-3) |
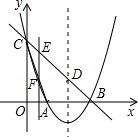 如图.抛物线y=x2+bx+c与y轴交于点C(0,3),与x轴交于A,B两点,A点在对称轴的左侧,B点的坐标为(3,0).
如图.抛物线y=x2+bx+c与y轴交于点C(0,3),与x轴交于A,B两点,A点在对称轴的左侧,B点的坐标为(3,0).