题目内容
19.计算:(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$
(2)($\sqrt{6}$-$\sqrt{5}$)($\sqrt{6}$+$\sqrt{5}$)+(2$\sqrt{3}$-3$\sqrt{2}$)2.
分析 (1)首先化简二次根式进而合并求出答案;
(2)直接利用乘法公式进而化简求出答案.
解答 解:(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$
=4$\sqrt{3}$-6×$\frac{\sqrt{3}}{3}$+3×4$\sqrt{3}$
=2$\sqrt{3}$+12$\sqrt{3}$
=14$\sqrt{3}$;
(2)($\sqrt{6}$-$\sqrt{5}$)($\sqrt{6}$+$\sqrt{5}$)+(2$\sqrt{3}$-3$\sqrt{2}$)2
=6-5+12+18-12$\sqrt{6}$
=31-12$\sqrt{6}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.下列多项式中,能直接用公式法分解因式的是( )
| A. | x2-xy2 | B. | x2+xy+y2 | C. | 4x2-4x-1 | D. | x2-4x+4 |
7.抛物线y=x2+2的对称轴是( )
| A. | 直线x=0 | B. | 直线x=1 | C. | 直线x=1 | D. | 直线x=2 |
8.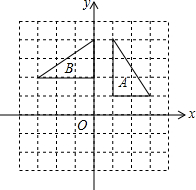 如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )
如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )
 如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )
如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )| A. | (0,1) | B. | (-1,0) | C. | (0,0) | D. | (-2,-1) |