题目内容
7．
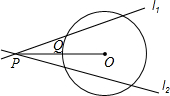如图，点P为⊙O外一点，连结OP交⊙O于点Q，且PQ=OQ，经过点P的直线l1，l2，都与⊙O相交，则l1与l2所成的锐角α的取值范围是（ ）| A． | 0°＜α＜30° | B． | 0°＜α＜45° | C． | 0°＜α＜60° | D． | 0°＜α＜90° |
分析 根据切线的性质和直角三角形的性质求出∠OPA，解答即可．
解答 解：当直线l1，l2，都与⊙O相切时，切点分别为A、B，连接OA，
则OA⊥l1，
∵OA=OQ=PQ，
∴∠OPA=30°，
∴l1与l2所成的锐角α小于60°，
故选：C．
点评 本题考查的是直线和圆的三种位置关系，掌握切线的性质、直角三角形的性质是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
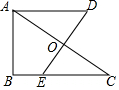如图，Rt△ABC，∠B=90°，AC的垂直平分线交BC于点E，垂足为点O，过点A作BC的平行线，与直线OE交于点D，若AB=4，BC=6，则AD的长为$\frac{13}{3}$．
如图，抛物线y=ax2+bx+3经过A（-1，0），B（3，0）两点，与y轴相交于点C，点P是抛物线上一点，过点P作PD∥y轴交线段BC干点D．
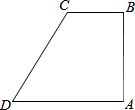如图，在四边形ABCD中，AB⊥BC，AD∥BC，∠BCD=120°，BC=2，AD=DC．P为四边形ABCD边上的任意一点，当∠BPC=30°时，CP的长为2或2$\sqrt{3}$或4．
某居民小区一处柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，如图是水平放置的破裂管道有水部分的截面．