题目内容
17. 某居民小区一处柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
某居民小区一处柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.(1)请你用直尺和圆规补全这个输水管道的圆形截面(保留作图痕迹);
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
分析 (1)根据尺规作图的步骤和方法作出图即可;
(2)先过圆心O作半径CO⊥AB,交AB于点D设半径为r,得出AD、OD的长,在Rt△AOD中,根据勾股定理求出这个圆形截面的半径.
解答  解:(1)如图所示;
解:(1)如图所示;
(2)作OC⊥AB于C,并延长交⊙O于D,则C为AB的中点,
∵AB=16cm,
∴AD=$\frac{1}{2}$AB=8cm.
设这个圆形截面的半径为xcm,
又∵CD=4cm,
∴OC=x-4,
在Rt△OAD中,
∵OD2+AD2=OA2,即(x-4)2+82=x2,
解得x=10.
∴这个圆形截面的半径为10cm.
点评 此题考查的是作图-应用与设计作图,涉及到垂经定理和勾股定理,关键是根据题意画出图形,再根据勾股定理进行求解.

练习册系列答案
相关题目
7.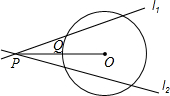 如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )
如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )
 如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )
如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )| A. | 0°<α<30° | B. | 0°<α<45° | C. | 0°<α<60° | D. | 0°<α<90° |
12.3月12日是我国的植树节,这天有20位同学共植树52棵,其中男生每人植树3棵,女生每人植树2棵,若设男生有x人,女生有y人,则根据题意列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=52}\\{3x+2y=20}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=52}\\{2x+3y=20}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=20}\\{2x+3y=52}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=20}\\{3x+2y=52}\end{array}\right.$ |
2.某商店有2个进价不同的计算器都卖了80元,其中一个盈利60%,另一个亏本20%,在这笔买卖中,这家商店( )
| A. | 赚了10元 | B. | 赔了10元 | C. | 不赔不赚 | D. | 赚了8元 |
7.把$\sqrt{18}$化成最简二次根式,结果为( )
| A. | $2\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $3\sqrt{6}$ | D. | $9\sqrt{2}$ |
 已知:如图AB⊥BD,CD⊥BD,AB=DC,求证:AD∥BC.
已知:如图AB⊥BD,CD⊥BD,AB=DC,求证:AD∥BC.