题目内容
13.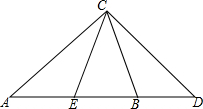 如图,点A、E、B、D在同一条直线上,AE=DB,∠A=∠D,∠CED=∠CBA,试判断△ACE与△CDB是否全等,并说明理由.
如图,点A、E、B、D在同一条直线上,AE=DB,∠A=∠D,∠CED=∠CBA,试判断△ACE与△CDB是否全等,并说明理由.
分析 根据补角的性质得到∠AEC=∠DBC,然后根据全等三角形的判定即可证得结论.
解答 解:△ACE与△CDB全等,
理由:∵∠CED=∠CBA,
∴180°-∠CED=180°-∠CBA,
即:∠AEC=∠DBC,
在△AEC与△DBC中,
$\left\{\begin{array}{l}{∠A=∠D}\\{AE=DB}\\{∠AEC=∠DBC}\end{array}\right.$,
∴△ACE≌△CDB.
点评 本题考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
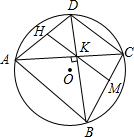 如图.在⊙O的内接四边形ABCD中,AC⊥BD,垂足为K,M是BC的中点,直线MK交AD于点H.KH与AD有怎样的位置关系?为什么?
如图.在⊙O的内接四边形ABCD中,AC⊥BD,垂足为K,M是BC的中点,直线MK交AD于点H.KH与AD有怎样的位置关系?为什么? 已知:如图,∠BCA=∠DAC.求证:∠B与∠DAB互补.
已知:如图,∠BCA=∠DAC.求证:∠B与∠DAB互补.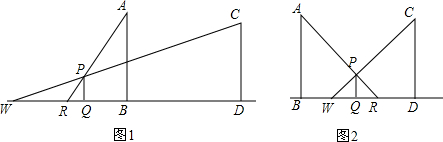
 抛物线y=x2-x-6与x轴交于点A、B(A在B的左边),与y轴分别交于点C.
抛物线y=x2-x-6与x轴交于点A、B(A在B的左边),与y轴分别交于点C.