题目内容
16.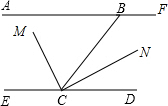 如图:AF∥DE,B为AF上的一点,∠ABC=60°交ED于C,CM平分∠BCE,∠MCN=90°,
如图:AF∥DE,B为AF上的一点,∠ABC=60°交ED于C,CM平分∠BCE,∠MCN=90°,(1)∠DCN的度数;
(2)若∠CBF的平分线交CN于N,求证:BN∥CM.
分析 (1)根据平行线性质求出∠BCE=120°,∠BCD=∠ABC=60°,求出∠MCB=60°,∠BCN=30°,即可求出答案;
(2)作∠FBC的角平分线BN,交CN于N,求出∠NBC=∠BCM即可.
解答 解:(1)∵AF∥DE,∠ABC=60°,
∴∠BCE=180°-60°=120°,∠BCD=∠ABC=60°,
∵CM平分∠BCE,
∴∠MCB=60°,
∵∠MCN=90°,
∴∠BCN=90°-60°=30°,
∴∠DCN=60°-30°=30°;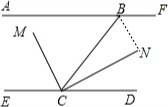
(2)作∠FBC的角平分线BN,交CN于N,
∵∠ABC=60°,
∴∠FBC=120°,
∵BN平分∠FBC,
∴∠NBC=60°,
∵∠BCM=60°,
∴∠NBC=∠BCM,
∴BN∥CM.
点评 本题考查了平行线的性质和判定,角平分线定义的应用,能运用平行线的判定和性质进行推理是解此题的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
4.实数3.14159,4.$\stackrel{••}{21}$,$\frac{22}{7}$,$\sqrt{3}$,π-3.14,$\sqrt{25}$,0.1010010001…中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
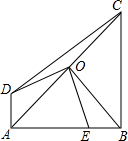 如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC=4,O为AC的中点,OE⊥OD交AB于点E.若AE=3,则OD的长为$\sqrt{5}$.
如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC=4,O为AC的中点,OE⊥OD交AB于点E.若AE=3,则OD的长为$\sqrt{5}$.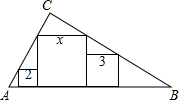 如图,在直角三角形ABC中(∠C=90°),放置边长分别为2、x、3的三个正方形,则x的值为5.
如图,在直角三角形ABC中(∠C=90°),放置边长分别为2、x、3的三个正方形,则x的值为5.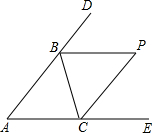 如图,△ABC的∠ABC、∠ACB的外角的平分线交于点P.
如图,△ABC的∠ABC、∠ACB的外角的平分线交于点P.