题目内容
8.化简:$\frac{\sqrt{2}+\sqrt{3}}{\sqrt{10}+\sqrt{14}+\sqrt{15}+\sqrt{21}}$.分析 我们可以先将分母因式分解,约分后再化简.
解答 解:$\frac{\sqrt{2}+\sqrt{3}}{\sqrt{10}+\sqrt{14}+\sqrt{15}+\sqrt{21}}$
=$\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}(\sqrt{5}+\sqrt{7})+\sqrt{3}(\sqrt{5}+\sqrt{7})}$,
=$\frac{\sqrt{2}+\sqrt{3}}{(\sqrt{2}+\sqrt{3})(\sqrt{5}+\sqrt{7})}$,
=$\frac{1}{\sqrt{5}+\sqrt{7}}$,
=$\frac{\sqrt{7}-\sqrt{5}}{2}$.
点评 此题主要考查分母有理化,把分母分组分解是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.
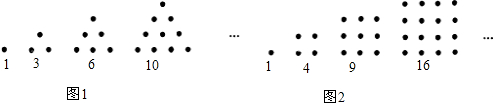
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
(1)按照规律,表格中a=28,b=36,c=35.
(2)观察表中规律,第n个“正方形数”是n2;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是n2+x-n.
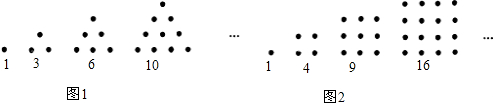
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
| 三角形数 | 1 | 3 | 6 | 10 | 15 | 21 | a | … |
| 正方形数 | 1 | 4 | 9 | 16 | 25 | b | 49 | … |
| 五边形数 | 1 | 5 | 12 | 22 | C | 51 | 70 | … |
(2)观察表中规律,第n个“正方形数”是n2;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是n2+x-n.
19.若x2-2kx+25是一个完全平方式,则k=( )
| A. | 10 | B. | ±10 | C. | 5 | D. | ±5 |
13.以菱形ABCD的一个顶点A为圆心,以边AB长为半径画圆,被菱形截得的$\widehat{BD}$是40°,则菱形的一个钝角是( )
| A. | 140° | B. | 160° | C. | 100° | D. | 150° |
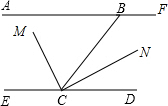 如图:AF∥DE,B为AF上的一点,∠ABC=60°交ED于C,CM平分∠BCE,∠MCN=90°,
如图:AF∥DE,B为AF上的一点,∠ABC=60°交ED于C,CM平分∠BCE,∠MCN=90°,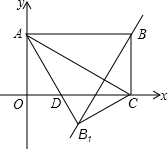 如图,矩形OABC在平面直角坐标系中,并且OA、OC的长满足:|OA-2$\sqrt{3}$|+(OC-6)2=0.
如图,矩形OABC在平面直角坐标系中,并且OA、OC的长满足:|OA-2$\sqrt{3}$|+(OC-6)2=0.