题目内容
7.如图所示,在平面直角坐标系中,⊙P的圆心在x轴上,其坐标为(40,0),⊙P的半径是20,在Rt△ABC中,∠ACB=90°,A(0,12)、C(0,-12)、B(-18,-12),将Rt△ABC沿x轴向右平移m(0<m<40)个单位长度得到△DEF,使得D、F两点落在圆上,期中A、B、C三点分别与D、E、F三点对应,DE、DF分别交x轴于点H、G(1)求Rt△ABC移动的距离m;
(2)判断直线DE与⊙P的位置关系,并证明你的结论.
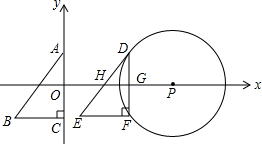
分析 (1)利用平移的性质结合勾股定理得出PG的长,进而得出答案;
(2)利用切线的判定方法,得出DH2+DP2=PH2,利用勾股定理逆定理得出答案.
解答 解:(1)连接DP,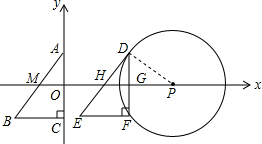 ∵A(0,12),C(0,-12),
∵A(0,12),C(0,-12),
∴AC⊥x轴,
∵DEF是由△ABC平移得到的,
∴DF⊥x轴,DF=AC=24,
∴DG=$\frac{1}{2}$DF=12,
在Rt△DGP中,DP=20,
∴PG=$\sqrt{2{0}^{2}-1{2}^{2}}$=16,
∴m=OG=40-16=24;
(2)直线DE与⊙P相切,
理由:设AB交x轴于点M,
∵A(0,12),B(-18,-12),C(0,-12),
∴BC=18,OA=OC=12,AC⊥x轴,
∵∠ACB=90°,
∴OM∥BC,
∴OM=$\frac{1}{2}$BC=9,
∵△DEF是由△ABC平移得到的,
∴HG=OM=9,HP=HG+GP=9+16=25,
在Rt△DGH中,DH=$\sqrt{D{G}^{2}+G{H}^{2}}$=$\sqrt{1{2}^{2}+{9}^{2}}$=15,
∵202+152=252,
∴DH2+DP2=PH2,
∴PD⊥DE,
∴直线DE与⊙P相切.
点评 此题主要考查了圆的综合以及勾股定理、切线的判定等知识,正确利用勾股定理得出PG的长是解题关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
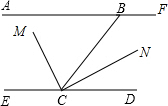 如图:AF∥DE,B为AF上的一点,∠ABC=60°交ED于C,CM平分∠BCE,∠MCN=90°,
如图:AF∥DE,B为AF上的一点,∠ABC=60°交ED于C,CM平分∠BCE,∠MCN=90°,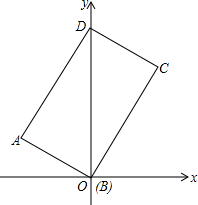 如图,矩形ABCD的对角线BD和y轴重合,已知AB=3,BC=3$\sqrt{3}$,求矩形各顶点的坐标.
如图,矩形ABCD的对角线BD和y轴重合,已知AB=3,BC=3$\sqrt{3}$,求矩形各顶点的坐标.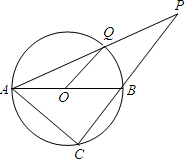 如图,过圆O外一点P作圆O的两条割线PA、PC分别交圆O于Q、A,B、C,且OQ∥PC,圆O的半径是3cm.
如图,过圆O外一点P作圆O的两条割线PA、PC分别交圆O于Q、A,B、C,且OQ∥PC,圆O的半径是3cm.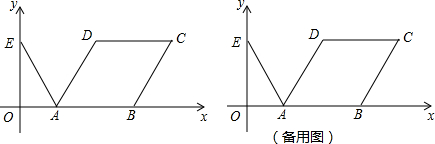
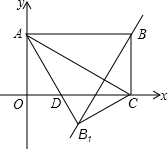 如图,矩形OABC在平面直角坐标系中,并且OA、OC的长满足:|OA-2$\sqrt{3}$|+(OC-6)2=0.
如图,矩形OABC在平面直角坐标系中,并且OA、OC的长满足:|OA-2$\sqrt{3}$|+(OC-6)2=0.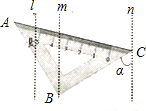 如图,直线l∥m∥n,△ABC的直角顶点B和另一顶点C分别在直线m和n上,边BC与直线n所夹的角∠α为52°,则∠β的度数为38°.
如图,直线l∥m∥n,△ABC的直角顶点B和另一顶点C分别在直线m和n上,边BC与直线n所夹的角∠α为52°,则∠β的度数为38°.