题目内容
16.对于正整数n,定义F(n)=$\left\{\begin{array}{l}{{n}^{2},n<10}\\{f(n),n≥10}\end{array}\right.$,其中f(n)表示n的首位数字、末位数字的平方和.例如:F(6)=62=36,F(123)=f(123)=12+32=10.规定F1(n)=F(n),Fk+1(n)=F(Fk(n)).例如:F1(123)=F(123)=10,F2(123)=F(F1(123))=F(10)=1.(1)求:F2(4)=37,F2015(4)=26;
(2)若F3m(4)=89,则正整数m的最小值是6.
分析 通过观察前8个数据,可以得出规律,这些数字7个一个循环,根据这些规律计算即可.
解答 解:(1)F2(4)=F(F1(4))=F(16)=12+62=37;
F1(4)=F(4)=16,F2(4)=37,F3(4)=58,
F4(4)=89,F5(4)=145,F6(4)=26,F7(4)=40,F8(4)=16,
通过观察发现,这些数字7个一个循环,2015是7的287倍余6,因此F2015(4)=26;
(2)由(1)知,这些数字7个一个循环,F4(4)=89=F18(4),因此3m=18,所以m=6.
故答案为:(1)37,26;(2)6.
点评 本题属于数字变化类的规律探究题,通过观察前几个数据可以得出规律,熟练找出变化规律是解题的关键.

练习册系列答案
相关题目
8.下列分解因式,错误的是( )
| A. | m2-16=(m+4)(m-4) | B. | m2+3m+9=(m+3)2 | C. | m2-8m+16=(m-4)2 | D. | m2+4m=m(m+4) |
 已知,如图,在△ABC中和△A′B′C′中,∠BAC=∠B′A′C′,AB=A′B′,AD和A′D′分别是△ABC和△A′B′C′的角平分线,且AD=A′D′,求证:△ABC≌△A′B′C′.
已知,如图,在△ABC中和△A′B′C′中,∠BAC=∠B′A′C′,AB=A′B′,AD和A′D′分别是△ABC和△A′B′C′的角平分线,且AD=A′D′,求证:△ABC≌△A′B′C′.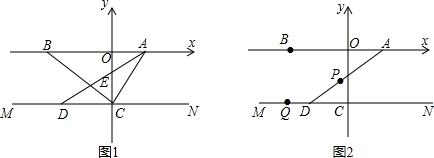
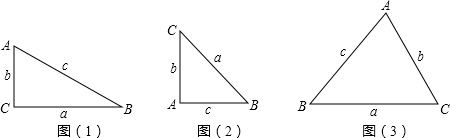
 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为多少度?
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为多少度?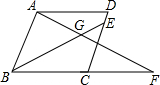 如图,菱形ABCD,∠ABC=60°,动点E、F分别从C点与B点出发,速度同为1单位/s,AB=4,F点先出发,若AF、BE相交于G,且∠AGB=60°时,问动点F与动点E出发时间有什么关系.此时$\frac{AF}{BE}$为多少?
如图,菱形ABCD,∠ABC=60°,动点E、F分别从C点与B点出发,速度同为1单位/s,AB=4,F点先出发,若AF、BE相交于G,且∠AGB=60°时,问动点F与动点E出发时间有什么关系.此时$\frac{AF}{BE}$为多少?