题目内容
6.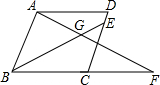 如图,菱形ABCD,∠ABC=60°,动点E、F分别从C点与B点出发,速度同为1单位/s,AB=4,F点先出发,若AF、BE相交于G,且∠AGB=60°时,问动点F与动点E出发时间有什么关系.此时$\frac{AF}{BE}$为多少?
如图,菱形ABCD,∠ABC=60°,动点E、F分别从C点与B点出发,速度同为1单位/s,AB=4,F点先出发,若AF、BE相交于G,且∠AGB=60°时,问动点F与动点E出发时间有什么关系.此时$\frac{AF}{BE}$为多少?
分析 先证明△ABC是等边三角形,得出AC=BC,∠ACB=60°,再证明△BCE≌△ACF,得出对应边相等CE=CF,BE=AF,即可得出结果.
解答 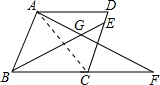 解:连接AC,如图所示:
解:连接AC,如图所示:
∵四边形ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,∠BCE=120°,
∴AC=BC,∠ACB=60°,
∴∠ACF=120°,
∴∠ACF=∠BCE,
∵∠AGB=60°,∠AGB=∠CBE+∠F,∠ACB=∠CAF+∠F,
∴∠CBE=∠CAF,
在△BCE和△ACF中,
$\left\{\begin{array}{l}{∠CBE=∠CAF}&{\;}\\{BC=AC}&{\;}\\{∠BCE=∠ACF}&{\;}\end{array}\right.$,
∴△BCE≌△ACF(ASA),
∴CE=CF,BE=AF,
∴BC+CE-CF=BC=4,
∴E、F出发时间相差4s,$\frac{AF}{BE}$=1.
点评 本题考查了菱形的性质、全等三角形的判定与性质、等边三角形的判定与性质;证明等边三角形和全等三角形是解决问题的关键.

练习册系列答案
相关题目
17. 如图,已知直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α等于( )
如图,已知直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α等于( )
 如图,已知直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α等于( )
如图,已知直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α等于( )| A. | 2l° | B. | 30° | C. | 58° | D. | 48° |
11.“把弯曲的公路改直,就能缩短路程”其中蕴含的数学道理是( )
| A. | 两点确定一条直线 | B. | 两点之间直线最短 | ||
| C. | 两点之间线段最短 | D. | 直线比曲线短 |
18.将一元二次方程x2-4x+3=0化成(x+m)2=n的形式,则n等于( )
| A. | -3 | B. | 1 | C. | 4 | D. | 7 |
 已知,如图,点D.E分别在AB、AC上,点F在BC的延长线上,∠A=35°,∠ACF=105°,∠ADE=70°.求证:DE∥BF.
已知,如图,点D.E分别在AB、AC上,点F在BC的延长线上,∠A=35°,∠ACF=105°,∠ADE=70°.求证:DE∥BF.