题目内容
1. 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为多少度?
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为多少度?
分析 先根据OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOB=40°,∠COE=60°求出∠BOC与∠COD的度数,再根据∠BOD=∠BOC+∠COD即可得出结论.
解答 解:∵OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOB=40°,∠COE=60°,
∴∠BOC=∠AOB=40°,∠COD=$\frac{1}{2}$∠COE=$\frac{1}{2}$×60°=30°,
∴∠BOD=∠BOC+∠COD=40°+30°=70°.
点评 本题考查的是角平分线的定义和角的和差计算,熟知角平分线的定义是解答此题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
10.在-1,0,3和$\sqrt{2}$这四个实数中,负数是( )
| A. | -1 | B. | 0 | C. | 3 | D. | $\sqrt{2}$ |
10.下列各组单项式中,不是同类项的是( )
| A. | -2与5 | B. | 6a2mb与-a2bm | C. | 2abx3与$-\frac{5}{6}ba{x^3}$ | D. | $\frac{1}{2}{x^3}y$与$-\frac{1}{2}x{y^3}$ |
11.“把弯曲的公路改直,就能缩短路程”其中蕴含的数学道理是( )
| A. | 两点确定一条直线 | B. | 两点之间直线最短 | ||
| C. | 两点之间线段最短 | D. | 直线比曲线短 |
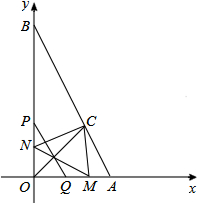 如图,在平面直角坐标系中,点A(2,0)、B(0,4),∠AOB的平分线交AB于点C,动点P从点O出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,PQ∥AB,交x轴于点Q,过点P、Q作关于直线OC的对称点M,N,连接MC、NC、MN,设点P运动的时间为t(0<t<2).
如图,在平面直角坐标系中,点A(2,0)、B(0,4),∠AOB的平分线交AB于点C,动点P从点O出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,PQ∥AB,交x轴于点Q,过点P、Q作关于直线OC的对称点M,N,连接MC、NC、MN,设点P运动的时间为t(0<t<2).