题目内容
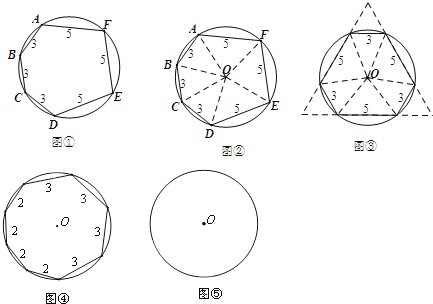
4．若同一个圆的内接正三角形、正方形、正六边形的边长分别记作a3，a4，a6，则a3：a4：a6等于（ ）| A． | 1：$\sqrt{2}$：$\sqrt{3}$ | B． | 1：2：3 | C． | 3：2：1 | D． | $\sqrt{3}$：$\sqrt{2}$：1 |
分析 从中心向边作垂线，构建直角三角形，通过解直角三角形可得．
解答 解：设圆的半径是r，
则多边形的半径是r，
如图1，则内接正三角形的边长a3=2rsin60°=$\sqrt{3}$r，
如图2，内接正方形的边长是a4=2rsin45°=$\sqrt{2}$r，
如图3，正六边形的边长是a6=r，
因而半径相等的圆的内接正三角形、正方形、正六边形的边长之比a3：a4：a6=$\sqrt{3}$：$\sqrt{2}$：1．
故选D．
点评 本题考查了正多边形和圆，正多边形的计算一般是通过中心作边的垂线，连接半径，把正多边形中的半径，边长，边心距，中心角之间的计算转化为解直角三角形．
练习册系列答案
相关题目
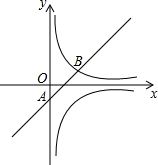如图，已知直线l经过点A（0，-1），与双曲线y=$\frac{m}{x}$（x＞0）交于点B（2，1）．点P在线段AB上，过点P作x轴的垂线分别交双曲线y=$\frac{m}{x}$（x＞0）和y=-$\frac{m}{x}$（x＞0）于点M、N．
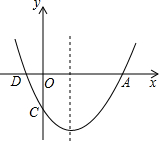如图，二次函数y=ax2+bx+c的图象与x轴的交点为A、D（A在D的右侧），与y轴的交点为C，且A（4，0）．C（0，-3），对称轴是直线x=l．
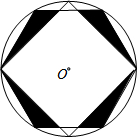如图，在半径为2的⊙O中，两个顶点重合的内接正四边形与正六边形，则阴影部分的面积为6-2$\sqrt{3}$．
如图，点D在△ABC的边BC上，∠C+∠BAD=∠DAC，tan∠BAD=$\frac{4}{7}$，AD=$\sqrt{65}$，CD=13，则线段AC的长为4$\sqrt{13}$．
如图，在直角坐标系xOy中，点A，B分别在x轴和y轴，$\frac{OA}{OB}$=$\frac{3}{4}$．∠AOB的角平分线与OA的垂直平分线交于点C，与AB交于点D，反比例函数y=$\frac{k}{x}$的图象过点C．当以CD为边的正方形的面积为$\frac{2}{7}$时，k的值是（ ）