题目内容
 如图,在△ABC中,AB=12cm,BC=8cm,BD平分∠ABC交AC于点D,DE∥BC交AB于点E.(1)求证:BE=ED;
如图,在△ABC中,AB=12cm,BC=8cm,BD平分∠ABC交AC于点D,DE∥BC交AB于点E.(1)求证:BE=ED;(2)求AE的长.
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:(1)利用角平分线的性质和平行线的性质证明∠EDB=∠EBD即可;
(2)由DE∥BC,可得△AED∽△ABC,设ED=x,利用相似得比例式
=
代入数据计算即可.
(2)由DE∥BC,可得△AED∽△ABC,设ED=x,利用相似得比例式
| DE |
| BC |
| AE |
| AB |
解答:证明:(1)∵BD平分∠ABC交AC于点D,
∴∠ABD=∠DBC,
∵DE∥BC,
∴∠EDB=∠DBC,
∴∠EDB=∠EBD,
∴BE=ED;
(2)∵DE∥BC,
∴△AED∽△ABC,
∴
=
,
设DE=xcm,则AE=12-x(cm),
∴
=
解得:x=4.8,
∴AE=12-x=7.2.
故AE的长是7.2cm.
∴∠ABD=∠DBC,
∵DE∥BC,
∴∠EDB=∠DBC,
∴∠EDB=∠EBD,
∴BE=ED;
(2)∵DE∥BC,
∴△AED∽△ABC,
∴
| DE |
| BC |
| AE |
| AB |
设DE=xcm,则AE=12-x(cm),
∴
| x |
| 8 |
| 12-x |
| 12 |
解得:x=4.8,
∴AE=12-x=7.2.
故AE的长是7.2cm.
点评:本题考查了平行线的性质、角平分线的定义、相似三角形的判定和性质,解题的关键是证明BE=ED.

练习册系列答案
相关题目
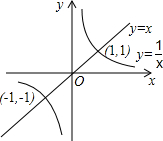 我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙.比如,通过图中的信息我们可以得出x>
我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙.比如,通过图中的信息我们可以得出x>| 1 |
| x |
| A、x>1 |
| B、-1<x<0 |
| C、x>1或-1<x<0 |
| D、以上都不对 |
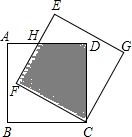 如图,边长为3的正方形ABCD终点C按顺时针旋转30°,得到正方形EFCG,交AD于点H,则阴影部分的面积为
如图,边长为3的正方形ABCD终点C按顺时针旋转30°,得到正方形EFCG,交AD于点H,则阴影部分的面积为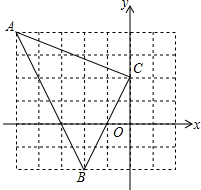 已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长.
已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长. 如图,线段AB上有一点C,且AC=2BC,D是AB中点,已知CD长为2cm,求BC、AB的长.
如图,线段AB上有一点C,且AC=2BC,D是AB中点,已知CD长为2cm,求BC、AB的长.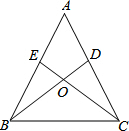 已知:如图,在△ABC中,AB=AC,点D,E分别在边AC,AB上,且∠ABD=∠ACE.BD与CE相交于点O.求证:(1)OB=OC;(2)BE=CD.
已知:如图,在△ABC中,AB=AC,点D,E分别在边AC,AB上,且∠ABD=∠ACE.BD与CE相交于点O.求证:(1)OB=OC;(2)BE=CD.
 直线在AB、CD相交于点O,OE平分∠BOD,若∠AOD:∠DOE=7:1,求∠AOC的度数.
直线在AB、CD相交于点O,OE平分∠BOD,若∠AOD:∠DOE=7:1,求∠AOC的度数.