题目内容
17.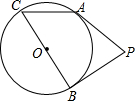 如图,点P在⊙O外,PA、PB是⊙O的切线,A、B是切点,BC是直径,若∠APB=70°,则∠ACB的度数为55°.
如图,点P在⊙O外,PA、PB是⊙O的切线,A、B是切点,BC是直径,若∠APB=70°,则∠ACB的度数为55°.
分析 连接OA,根据切线的性质得出∠PAO=∠PBO=90°,求出∠AOB=110°,根据三角形外角性质和等腰三角形性质求出即可.
解答 解: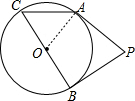
连接OA,
∵PA、PB是⊙O的切线,A、B是切点,
∴∠PAO=∠PBO=90°,
∵∠APB=70°,
∴∠AOB=360°-90°-90°-70°=110°,
∴∠ACB+∠OAC=∠AOB=110°,
∵OC=OA,
∴∠ACB=∠OAC,
∴∠ACB=55°
故答案为:55°.
点评 本题考查了切线的性质,三角形外角性质,等腰三角形性质的应用,能根据切线的性质求出∠PAO=∠PBO=90°是解此题的关键,注意:圆的切线垂直于过切点的半径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列各式中,能用平方差公式计算的是( )
| A. | (2a+b)(a-b) | B. | (-a-b)(-a+b) | C. | (a+b)(-a-b) | D. | (-a+b)(a-b) |
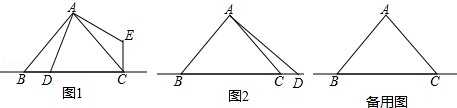
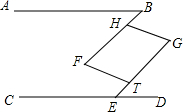 如图,已知AB∥CD,∠B=∠GED,∠F=∠G,试判断BF与GE有怎样的位置关系?HG与FT呢?请说明理由.
如图,已知AB∥CD,∠B=∠GED,∠F=∠G,试判断BF与GE有怎样的位置关系?HG与FT呢?请说明理由.