题目内容
5.已知直线y=kx+b与直线y=$\frac{1}{2}$x-1平行,且经过点(0,3),那么该直线的表达式是y=$\frac{1}{2}$x+3.分析 由两直线平行可得出k=$\frac{1}{2}$,根据直线上一点的坐标利用一次函数图象上点的坐标特征即可求出b值,此题得解.
解答 解:∵直线y=kx+b与直线y=$\frac{1}{2}$x-1平行,
∴k=$\frac{1}{2}$,b≠-1.
∵直线y=$\frac{1}{2}$x+b过点(0,3),
∴b=3.
故答案为:y=$\frac{1}{2}$x+3.
点评 本题考查了两条直线相交或平行问题以及一次函数图象上点的坐标特征,由两直线平行找出k=$\frac{1}{2}$、b≠-1是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
20. 如图,直线AB∥CD,∠A=115°,∠E=80°,则∠CDE的度数为( )
如图,直线AB∥CD,∠A=115°,∠E=80°,则∠CDE的度数为( )
 如图,直线AB∥CD,∠A=115°,∠E=80°,则∠CDE的度数为( )
如图,直线AB∥CD,∠A=115°,∠E=80°,则∠CDE的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
15.在下面的四个几何体中,它们各自的左视图与主视图不相同的是( )
| A. | 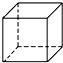 正方体 | B. | 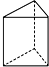 三棱柱 | C. | 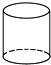 圆柱 | D. | 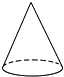 圆锥 |
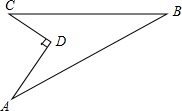 我校要对如图所示的一块地进行绿化,已知AD=4米,CD=3米,AD⊥DC,AB=13米,BC=12米,求这块地的面积.
我校要对如图所示的一块地进行绿化,已知AD=4米,CD=3米,AD⊥DC,AB=13米,BC=12米,求这块地的面积.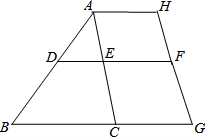 如图:已知∠DAE=55°,∠ADE=60°,∠ACB=65°,∠H与∠G互补,试说明AH∥DF的理由.
如图:已知∠DAE=55°,∠ADE=60°,∠ACB=65°,∠H与∠G互补,试说明AH∥DF的理由.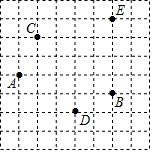 如图,在边长为1的小正方形组成的网格中,A、B、C、D、E五点都是格点.
如图,在边长为1的小正方形组成的网格中,A、B、C、D、E五点都是格点.