题目内容
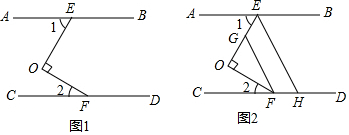
10. 如图:已知∠DAE=55°,∠ADE=60°,∠ACB=65°,∠H与∠G互补,试说明AH∥DF的理由.
如图:已知∠DAE=55°,∠ADE=60°,∠ACB=65°,∠H与∠G互补,试说明AH∥DF的理由.解:因为∠DAE+∠ADE+∠AED=180°(三角形内角和等于180°),
又∠DAE=55°,∠ADE=60°(已知),
所以∠AED=65°(等式性质).
因为∠ACB=65°(已知),
所以∠ACB=∠AED(等量代换),
所以DF∥BG(同位角相等,两直线平行),
因为∠H与∠G互补(已知),
所以∠H+∠G=180°,
所以AH∥BG(同旁内角互补,两直线平行),
所以AH∥DF(如果两条直线都与第三条直线平行,那么这两条直线平行).
分析 根据三角形内角和定理求出∠AED=65°°,求出∠ACB=∠AED,根据平行线的判定得出DF∥BG,AH∥BG,即可得出答案.
解答 解:∵∠DAE+∠ADE+∠AED=180°(三角形内角和等于180°),
又∵∠DAE=55°,∠ADE=60°(已知),
∴∠AED=65°(等式性质),
∵∠ACB=65°(已知),
∴∠ACB=∠AED(等量代换),
∴DF∥BG(同位角相等,两直线平行),
∵∠H与∠G互补,
∴∠H+∠G=180°(等式性质),
∴AH∥BG(同旁内角互补,两直线平行),
∴AH∥DF(如果两条直线都与第三条直线平行,那么这两条直线平行),
故答案为:三角形内角和等于180°,65,AED,同位角相等,两直线平行,同旁内角互补,两直线平行,如果两条直线都与第三条直线平行,那么这两条直线平行.
点评 本题考查了平行线的性质和判定,三角形内角和定理,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
 如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF.
如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF.
 解不等式组:$\left\{\begin{array}{l}{2-3x≥2x-8}\\{\frac{2-x}{3}-2<\frac{x-1}{2}}\end{array}\right.$,把它的解集在数轴上表示出来,并写出这个不等式组的整数解.
解不等式组:$\left\{\begin{array}{l}{2-3x≥2x-8}\\{\frac{2-x}{3}-2<\frac{x-1}{2}}\end{array}\right.$,把它的解集在数轴上表示出来,并写出这个不等式组的整数解. 如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).
如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).