题目内容
15.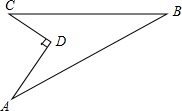 我校要对如图所示的一块地进行绿化,已知AD=4米,CD=3米,AD⊥DC,AB=13米,BC=12米,求这块地的面积.
我校要对如图所示的一块地进行绿化,已知AD=4米,CD=3米,AD⊥DC,AB=13米,BC=12米,求这块地的面积.
分析 连接AC,利用勾股定理可以得出三角形ACD和ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
解答  解:连接AC.
解:连接AC.
由勾股定理可知
AC=$\sqrt{A{D^2}+C{D^2}}$=$\sqrt{{4^2}+{3^2}}$=5,
又∵AC2+BC2=52+122=132=AB2,
∴△ABC是直角三角形,
故所求面积=△ABC的面积-△ACD的面积$\frac{1}{2}×5×12-\frac{1}{2}×3×4$=24(m2).
点评 考查了直角三角形面积公式以及勾股定理的应用,关键是作出辅助线得到直角三角形.

练习册系列答案
相关题目
7.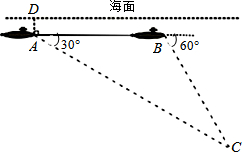 如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
 如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )| A. | 2000米 | B. | 4000米 | C. | 2000$\sqrt{3}$米 | D. | (2000$\sqrt{3}$+500)米 |
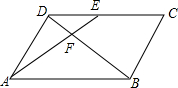 如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=1:2,FB=12,则DF=( )
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=1:2,FB=12,则DF=( )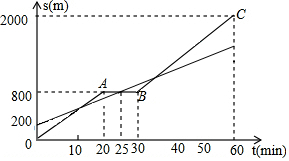 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象. 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF
 如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF.
如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF. 如图,在平面直角坐标系xOy中,二次函数y=x2-2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
如图,在平面直角坐标系xOy中,二次函数y=x2-2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.