题目内容
18.计算:(1)$\frac{2}{3}$x3y2•(-$\frac{3}{2}$xy2)2
(2)30+(-3)2-($\frac{1}{4}$)-1
(3)x(3x-y)-(3x-2y)2
(4)(2a-3b)2•(2a+3b)2.
分析 (1)原式利用幂的乘方与积的乘方运算法则计算,再利用单项式乘单项式法则计算即可得到结果;
(2)原式利用零指数幂、负整数指数幂法则,以及乘方的意义计算即可得到结果;
(3)原式利用单项式乘以多项式,以及完全平方公式化简,去括号合并即可得到结果;
(4)原式利用积的乘方运算法则变形,再利用平方差公式及完全平方公式化简即可得到结果.
解答 解:(1)原式=$\frac{2}{3}$x3y2•($\frac{9}{4}$x2y4)=$\frac{3}{2}$x5y6;
(2)原式=1+9-4=6;
(3)原式=3x2-xy-9x2+12xy-4y2=-6x2+11xy-4y2;
(4)原式=(4a2-9b2)2=16a4-72a2b2+81b4.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列分式中,是最简分式的是( )
| A. | $\frac{2a}{3{a}^{2}b}$ | B. | $\frac{x+y}{{x}^{2}+{y}^{2}}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{{a}^{2}+ab}{ab+{b}^{2}}$ |
8.将边长为1的正方形,按如图所示的方式分割,第1次分割后的阴影部分面积S1=$\frac{1}{2}$,第2次分割后的阴影部分面积S2=$\frac{3}{4}$,第3次分割后的阴影部分面S3=$\frac{7}{8}$,…,按照这样的规律分割,则第n(n为正整数)次分割后的阴影部分面积可用n表示为Sn=( )


| A. | $\frac{1}{{2}^{n}}$ | B. | 1-$\frac{1}{{2}^{n}}$ | C. | 1-$\frac{1}{{2}^{n+1}}$ | D. | 1-$\frac{1}{{2}^{n-1}}$ |
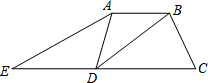 如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC=30°;延长CD到点E,连接AE,使得∠C=2∠E.
如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC=30°;延长CD到点E,连接AE,使得∠C=2∠E.
 证明定理:一组对边平行且相等的四边形是平行四边形.
证明定理:一组对边平行且相等的四边形是平行四边形. 如图,在△ABC中,AD是BC的中线,点E是AC上一点,BE交AD于点F,若AE=EF,求证:BF=AC.
如图,在△ABC中,AD是BC的中线,点E是AC上一点,BE交AD于点F,若AE=EF,求证:BF=AC.