题目内容
10.已知线段AB=4,点P是线段AB的黄金分割点,则AP的长为2$\sqrt{5}$-2或6-2$\sqrt{5}$.分析 把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比.
解答 解:当AP>BP时,
AP=$\frac{\sqrt{5}-1}{2}$AB=2$\sqrt{5}$-2,
当AP<BP时,AP=4-(2$\sqrt{5}$-2)=6-2$\sqrt{5}$,
故答案为:2$\sqrt{5}$-2或6-2$\sqrt{5}$.
点评 本题考查的是黄金分割的概念,把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比.

练习册系列答案
相关题目
15.某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到设计方案有等腰三角形,正三角形,等腰梯形和菱形四种图形,你认为符合条件的是( )
| A. | 等腰三角形 | B. | 正三角形 | C. | 等腰梯形 | D. | 菱形 |
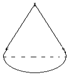
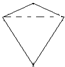
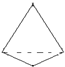
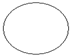
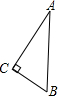 将如图所示放置的一个直角三角形ABC,(∠C=90°),绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图中的( )
将如图所示放置的一个直角三角形ABC,(∠C=90°),绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图中的( )