题目内容
13.下列分式中,是最简分式的是( )| A. | $\frac{2a}{3{a}^{2}b}$ | B. | $\frac{x+y}{{x}^{2}+{y}^{2}}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{{a}^{2}+ab}{ab+{b}^{2}}$ |
分析 最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解答 解:A、原式可化简为$\frac{2}{3ab}$,故不是最简分式;
B、分子与分母没有公分母,是最简分式;
C、原式可化简为$\frac{1}{x+1}$,不是最简分式;
D、原式可化简为$\frac{a}{b}$,不是最简分式,
故选B.
点评 考查了最简分式的知识,分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.

练习册系列答案
相关题目
4.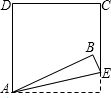 如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比大∠BAE大48°.设∠BAD和∠BAE的度数分别为x、y,那么x、y所适合的一个方程组是( )
如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比大∠BAE大48°.设∠BAD和∠BAE的度数分别为x、y,那么x、y所适合的一个方程组是( )
 如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比大∠BAE大48°.设∠BAD和∠BAE的度数分别为x、y,那么x、y所适合的一个方程组是( )
如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比大∠BAE大48°.设∠BAD和∠BAE的度数分别为x、y,那么x、y所适合的一个方程组是( )| A. | $\left\{\begin{array}{l}{y-x=48}\\{y+x=90}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-x=48}\\{y=2x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y-x=48}\\{y+2x=90}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=48}\\{x+2y=90}\end{array}\right.$ |
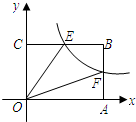 如图,y=$\frac{k}{x}$(x>0)经过矩形的边AB、BC的中点F、E,四边形OEBF的面积为2,则k=2.
如图,y=$\frac{k}{x}$(x>0)经过矩形的边AB、BC的中点F、E,四边形OEBF的面积为2,则k=2.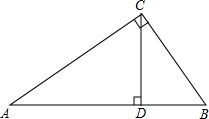 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=2,BD=1,则AD的长是4,AC的长是2$\sqrt{5}$.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=2,BD=1,则AD的长是4,AC的长是2$\sqrt{5}$.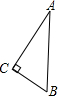 将如图所示放置的一个直角三角形ABC,(∠C=90°),绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图中的( )
将如图所示放置的一个直角三角形ABC,(∠C=90°),绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图中的( )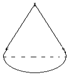
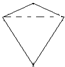
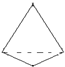
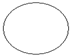
 如图,△ABC的点A的坐标是(3,4),点B的坐标是(1,2).
如图,△ABC的点A的坐标是(3,4),点B的坐标是(1,2).