题目内容
3. 如图,在△ABC中,AD是BC的中线,点E是AC上一点,BE交AD于点F,若AE=EF,求证:BF=AC.
如图,在△ABC中,AD是BC的中线,点E是AC上一点,BE交AD于点F,若AE=EF,求证:BF=AC.
分析 延长AD至G,使DG=AD,连接BG,可证明△BDG≌△CDA(SAS),则BG=AC,∠CAD=∠G,根据AE=EF,得∠CAD=∠AFE,可证出∠G=∠BFG,即得出AC=BF.
解答  证明:延长AD至G,使DG=AD,连接BG,
证明:延长AD至G,使DG=AD,连接BG,
在△BDG和△CDA中,
$\left\{\begin{array}{l}{BD=CD}\\{∠BDG=∠CDA}\\{DG=DA}\end{array}\right.$,
∴△BDG≌△CDA(SAS),
∴BG=AC,∠CAD=∠G
又∵AE=EF
∴∠CAD=∠AFE
又∠BFG=∠AFE
∴∠CAD=∠BFG
∴∠G=∠BFG
∴BG=BF,
∴AC=BF.
点评 本题考查了全等三角形的判定和性质,证明线段相等,一般转化为证明三角形的全等是解题关键.

练习册系列答案
相关题目
13.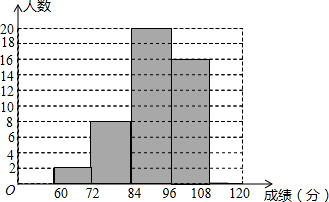 朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题.
朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题.
(1)频数分布表中a=0.4,b=4;
(2)补全频数分布直方图;
(3)为了激励学生,教师准备从超过108分的学生中选2人介绍学习经验,那么取得118分的小红和112分的小明同时被选上的概率是多少?请用列表法或画树形图加以说明,并列出所有可能的结果.
 朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题.
朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题. | 频数 | 频率 | |
| 60<x≤72 | 2 | 0.04 |
| 72<x≤84 | 8 | 0.16 |
| 84<x≤96 | 20 | a |
| 96<x≤108 | 16 | 0.32 |
| 108<x≤120 | b | 0.08 |
| 合计 | 50 | 1 |
(2)补全频数分布直方图;
(3)为了激励学生,教师准备从超过108分的学生中选2人介绍学习经验,那么取得118分的小红和112分的小明同时被选上的概率是多少?请用列表法或画树形图加以说明,并列出所有可能的结果.
14.多项式-$\frac{1}{3}$x|m|+(m-4)x+7是关于x的四次三项式,则m的值是( )
| A. | 4 | B. | -2 | C. | -4 | D. | 4或-4 |
15.某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到设计方案有等腰三角形,正三角形,等腰梯形和菱形四种图形,你认为符合条件的是( )
| A. | 等腰三角形 | B. | 正三角形 | C. | 等腰梯形 | D. | 菱形 |
12.为了解用电量的多少,李明在六月初连续一星期在同一时刻观察电表显示的度数,居民用电每度0.54元.记录如下:
这个星期李明家共用电28度,李明家这个星期的电费为15.12元.
| 日期 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 |
| 电表显示(度) | 117 | 120 | 124 | 129 | 135 | 138 | 142 | 145 |
13.|-25|的平方根为( )
| A. | 5 | B. | -5 | C. | 25 | D. | 5或-5 |