题目内容
20.计算.(1)$\frac{{\sqrt{2}}}{{\sqrt{2}+1}}$
(2)$3\sqrt{\frac{1}{3}}+\sqrt{24}÷\sqrt{2}$.
分析 (1)直接分母有理化进而化简求出答案;
(2)首先化简二次根式进而合并同类二次根式得出答案.
解答 解:(1)$\frac{{\sqrt{2}}}{{\sqrt{2}+1}}$=$\frac{\sqrt{2}(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=2-$\sqrt{2}$;
(2)$3\sqrt{\frac{1}{3}}+\sqrt{24}÷\sqrt{2}$
=3×$\frac{\sqrt{3}}{3}$+$\sqrt{12}$
=$\sqrt{3}$+2$\sqrt{3}$
=3$\sqrt{3}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
11.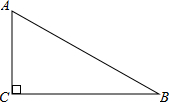 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | 4 | C. | 8$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
15.若0<a<1,下列比较a-1,a,a2的大小关系正确的是( )
| A. | a-1<a<a2 | B. | a<a-1<a2 | C. | a<a2<a-1 | D. | a2<a<a-1 |
5.如果把分式$\frac{2n}{{m}^{2}-{n}^{2}}$中的m和n都扩大2倍,那么分式的值( )
| A. | 不变 | B. | 扩大2倍 | C. | 缩小2倍 | D. | 扩大4倍 |
12.小明在相同条件下进行了绿豆的发芽试验,其不完整的结果如表所示:
那么表中m、n的值分别为m=382,n=0.956.
| 每批粒数 | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
| 发芽粒数 | 96 | 282 | m | 570 | 948 | 1912 | 2850 |
| 发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | n | 0.950 |
 如图,已知正方形ABCD的对角线长为$\sqrt{2}$,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为4.
如图,已知正方形ABCD的对角线长为$\sqrt{2}$,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为4.