题目内容
观察下列几个等式:
1+2+1=22=4
1+2+3+2+1=32=9
1+2+3+4+3+2+1=42=16
聪明的你一定能找出其中的规律,请利用其规律填空,
1+2+3+…+99+100+99+…+3+2+1= =
由此,我们又可利用上式得到求若干个连续自然数和的方法,思考后请运用知识解决问题:
(1)求1+2+3+…+99+100的值;
(2)由此可得:1+2+3+…+n= .
1+2+1=22=4
1+2+3+2+1=32=9
1+2+3+4+3+2+1=42=16
聪明的你一定能找出其中的规律,请利用其规律填空,
1+2+3+…+99+100+99+…+3+2+1=
由此,我们又可利用上式得到求若干个连续自然数和的方法,思考后请运用知识解决问题:
(1)求1+2+3+…+99+100的值;
(2)由此可得:1+2+3+…+n=
考点:规律型:数字的变化类
专题:规律型
分析:由已知等式得到1+2+3+…+99+100+99+…+3+2+1等于最中间数100的平方;
(1)先根据规律计算1+2+3+…+99+100+100+99+…+3+2+1得到10000+100,然后除以2即可;
(2)由(1)易得1+2+3+…+n=
(n2+n).
(1)先根据规律计算1+2+3+…+99+100+100+99+…+3+2+1得到10000+100,然后除以2即可;
(2)由(1)易得1+2+3+…+n=
| 1 |
| 2 |
解答:解:1+2+3+…+99+100+99+…+3+2+1=1002=10000;
(1)1+2+3+…+99+100+100+99+…+3+2+1=10000+100,
所以1+2+3+…+99+100=
(10000+100)=5000+50=5050;
(2)1+2+3+…+n=
(n2+n)=
故答案为1002,10000;
.
(1)1+2+3+…+99+100+100+99+…+3+2+1=10000+100,
所以1+2+3+…+99+100=
| 1 |
| 2 |
(2)1+2+3+…+n=
| 1 |
| 2 |
| n(n+1) |
| 2 |
故答案为1002,10000;
| n(n+1) |
| 2 |
点评:本题考查了规律型:数字的变化类:认真观察、仔细思考,善用联想是解决这类问题的方法,同时会从特殊向一般进行转化.

练习册系列答案
相关题目
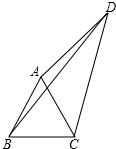 如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则△ACD的面积为
如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则△ACD的面积为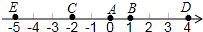 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动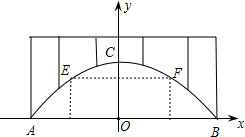 廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图,以水面AB所在直线为x轴,AB中点O为原点,建立平面直角坐标系.已知水面AB宽40米,抛物线最高点C到水面AB的距离为10米,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(结果保留根号)
廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图,以水面AB所在直线为x轴,AB中点O为原点,建立平面直角坐标系.已知水面AB宽40米,抛物线最高点C到水面AB的距离为10米,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(结果保留根号) 如图,在△ABC中,∠B=∠C,AD是BC边上的中线,E是AC上一点且DE=AE,求证:DE∥AB.
如图,在△ABC中,∠B=∠C,AD是BC边上的中线,E是AC上一点且DE=AE,求证:DE∥AB.