题目内容
关于x的不等式组
恰有两个整数解.则实数a的取值范围为 .
|
考点:一元一次不等式组的整数解
专题:
分析:先求出每个不等式的解集,再求出不等式组的解集,根据已知得出关于a的不等式组,求出即可.
解答:解:
由①得:x>-
,
由②得:x<2a,
所以不等式组的解集是-
<x<2a,
∵x的不等式组
恰有两个整数解,
∴1<2a≤2,
∴
<a≤1,
故答案为:
<a≤1.
|
由①得:x>-
| 2 |
| 5 |
由②得:x<2a,
所以不等式组的解集是-
| 2 |
| 5 |
∵x的不等式组
|
∴1<2a≤2,
∴
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了解一元一次不等式,解一元一次不等式组,不等式组的整数解的应用,解此题的关键是得出关于a的不等式组.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
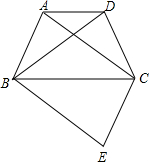 如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.