题目内容
16.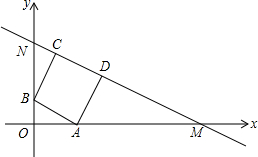 在直角坐标系中,直线MN分别交x轴、y轴的正半轴于点N、M,正方形ABCD内接于Rt△MON,点A、B分别在线段MO、NO上,点C、D在线段MN上.若点D的坐标为(7,4),则点C坐标(3,7).
在直角坐标系中,直线MN分别交x轴、y轴的正半轴于点N、M,正方形ABCD内接于Rt△MON,点A、B分别在线段MO、NO上,点C、D在线段MN上.若点D的坐标为(7,4),则点C坐标(3,7).
分析 由四边形ABCD为正方形,易证得△OAB≌△EDA≌△FDC,从而找到相等的线段,结合点D的坐标为(7,4),即可得出结论.
解答 解:过点D做DE垂直x轴于E点,过点D、C分别做x轴、y轴平行线,二者交于F点,如图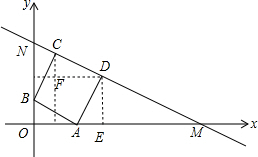
∵D(7,4),
∴DE=4,OE=7,
∵四边形ABCD为正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠BAD=90°,
∠OBA=180°-∠ABC-∠CBN=90°-∠CBN=∠CNB,
在△AOB和△BCN中,$\left\{\begin{array}{l}{∠BOA=∠NCB}\\{AB=BC}\\{∠OBA=∠CBN}\end{array}\right.$,
∴△AOB≌△BCN(ASA),
同理:△AOB≌△DEA,△CFD≌△BOA,
∴OA=ED=FD=4,OB=EA=FC,
∵OE=OA+AE,
∴CF=AE=OE-OA=7-4=3,
∴C点坐标为(OE-DF,DE+CF),即(3,7)
故答案为:(3,7).
点评 本题考查的全等三角形的判定和性质,解题的关键是利用△OAB≌△EDA≌△FDC,找到相等的线段.

练习册系列答案
相关题目
9. 如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=115°,则α=( )
如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=115°,则α=( )
 如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=115°,则α=( )
如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=115°,则α=( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
 某中学了解本校学生对球类运动的爱好情况,分为足球、篮球、排球、其他四个方面调查若干名学生,每人只选其中之一,统计后绘制成不完整的“折线统计图”(扇形统计图),根据信息解答下列问题:
某中学了解本校学生对球类运动的爱好情况,分为足球、篮球、排球、其他四个方面调查若干名学生,每人只选其中之一,统计后绘制成不完整的“折线统计图”(扇形统计图),根据信息解答下列问题: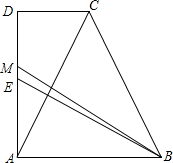 如图,直角梯形ABCD中,E为AD边上的中点,过A作AC⊥BE,交CD边于C,M是AD边上一点,且有BM=DM+AD,AD=BA.
如图,直角梯形ABCD中,E为AD边上的中点,过A作AC⊥BE,交CD边于C,M是AD边上一点,且有BM=DM+AD,AD=BA. 如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,以AD为直径作⊙O,⊙O分别交AB、AC于E、F.
如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,以AD为直径作⊙O,⊙O分别交AB、AC于E、F.