题目内容
4.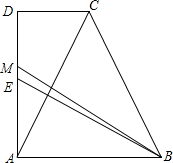 如图,直角梯形ABCD中,E为AD边上的中点,过A作AC⊥BE,交CD边于C,M是AD边上一点,且有BM=DM+AD,AD=BA.
如图,直角梯形ABCD中,E为AD边上的中点,过A作AC⊥BE,交CD边于C,M是AD边上一点,且有BM=DM+AD,AD=BA.(1)求证:CD=DE;
(2)求证:∠MBC=∠ABE.
分析 (1)根据AC⊥BE,求出∠AEB=∠ACD,推出△BAE≌△ADF,得出DC=AE,进一步得出答案即可;
(2)过点B作DC的垂线,垂足为点H,延长AD和BC交于点G,首先得出四边形ABHD是正方形,证△CDG≌△HCB和△ABE≌△CBH,结合BM=DM+AD,得出对应的角相等,整理得出结论即可.
解答 (1)证明:如图,
∵AC⊥BE,
∴∠AOE=90°,
∴∠EAC+∠AEB=90°,∠EAF+∠DCA=90°,
∴∠AEB=∠DCA,
在△BAE和△ADC中,
$\left\{\begin{array}{l}{∠BAE=∠D}\\{∠AEB=∠DCA}\\{AB=AD}\end{array}\right.$,
∴△BAE≌△ADC,
∴AE=CD,
∵E为AD边上的中点,
∴AE=DE,
∴CD=DE;
(2)证明:如图,
过点B作DC的垂线,垂足为点H,延长AD和BC交于点G,
∵∠ADC=∠DAB=∠H=90°,AD=AB,
∴四边形ABHD是正方形,
∴AD=DH=BH,
∵E为AD边上的中点,CD=DE,
∴D为HD边上的中点,
∴DC=DH,
在△CDG和△BHC中,
$\left\{\begin{array}{l}{∠CDG=∠H=90°}\\{DC=CH}\\{∠GCD=∠HCB}\end{array}\right.$,
∴△CDG≌△BHC,
∴GD=DH=AD,∠G=∠HBC,
∴BM=DM+AD=DM+DG=MG,
∴∠G=∠MBC,
∴∠HBC=∠MBC,
在△ABE和△BHC中,
$\left\{\begin{array}{l}{AB=BH}\\{∠EAB=∠H}\\{AE=CH}\end{array}\right.$,
∴△ABE≌△BHC,
∴∠ABE=∠HBC,
∴∠ABE=∠MBC.
点评 本题主要考查了全等三角形的性质和判定,正方形的判定与性质,等腰三角形的性质,综合运用性质进行证明是解此题的关键,注意辅助线的做法是解决问题的难点.

| A. | 50(1+x)2=146 | B. | 50+50(1+x)+50(1+x)2=146 | ||
| C. | 50(1+x)+50(1+x)2=146 | D. | 50+50(1+x)+50(1+2x)=146 |
 某工厂接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该工厂招收了新工人,设新工人王浩第x天生产的粽子数量为y只,y与x满足如下关系:
某工厂接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该工厂招收了新工人,设新工人王浩第x天生产的粽子数量为y只,y与x满足如下关系: (1)求作:△ABC,使AB=AC=a,∠B=∠α(保留作图痕迹,不写作法);
(1)求作:△ABC,使AB=AC=a,∠B=∠α(保留作图痕迹,不写作法);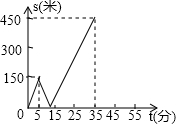 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示.
甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示.
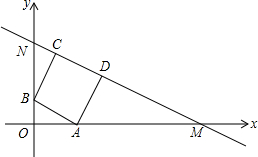 在直角坐标系中,直线MN分别交x轴、y轴的正半轴于点N、M,正方形ABCD内接于Rt△MON,点A、B分别在线段MO、NO上,点C、D在线段MN上.若点D的坐标为(7,4),则点C坐标(3,7).
在直角坐标系中,直线MN分别交x轴、y轴的正半轴于点N、M,正方形ABCD内接于Rt△MON,点A、B分别在线段MO、NO上,点C、D在线段MN上.若点D的坐标为(7,4),则点C坐标(3,7).