��Ŀ����
1����ͼ1����֪������y=-x2-4x+5��x���ڵ�A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C����DΪ�����ߵĶ��㣬����AD����1����ֱ��AD�Ľ���ʽ��
��2����E��m��0����F��m+1��0��Ϊx�������㣬���У�-5��m��-3.5��EE�䡢FF��ֱ�ƽ����y�ᣬ���������ڵ�E���F�䣬��AD�ڵ�M��N����ME��+NF���ֵ���ʱ����y������һ��R��ʹ��|RE��-RF��|ֵ����������R�����꼰|RE��-RF��|�����ֵ��
��3����ͼ2�������������Ƿ���ڵ�P��ʹ�á�PAC����ACΪ�ױߵĵ��������Σ������ڣ������P�����꼰��PAC��������������ڣ���˵�����ɣ�

���� ��1�����������ߵĽ���ʽ��õ�A��D�����꣬Ȼ�����ô���ϵ��������ֱ��AD�Ľ���ʽ���ɣ�
��2������ƽ���ߵ����ʺͺ���ͼ���ϵ������������ME��+NF��=-m2-7m-10-m2-9m-18=2m2-16m-28����϶��κ�����ֵ����������߶���̵õ���Ҫʹ|RE��-RF��|ֵ������E�䡢F�䡢R������һ��ֱ���ϣ�ֻ����õ�E�䡢F������꣬���ô���ϵ������ֱ֪��E��F���ϵʽ���ɸù�ϵʽ�����R�����꼴�ɣ�
��3����PA=PCʱ����P���߶�AC�Ĵ�ֱƽ�����ϣ���������ε������ʽ���н��
��� 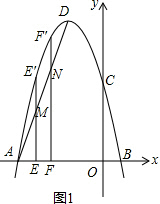 �⣺��1����ͼ1����y=-x2-4x+5=-��x+5����x-1����y=-��x+2��2+9��
�⣺��1����ͼ1����y=-x2-4x+5=-��x+5����x-1����y=-��x+2��2+9��
��A��-5��0����B��1��0����D��-2��9����
��ֱ��AD�Ľ���ʽΪ��y=kx+b��k��0������A��D��������룬��
$\left\{\begin{array}{l}{-5k+b=0}\\{-2k+b=9}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=3}\\{b=15}\end{array}\right.$��
��ֱ��AD�Ľ���ʽΪ��y=3x+15��
��2����ͼ1����EE���y�ᣬFF���y�ᣬE��m��0����F��m+1��0����
��E��m��-m2-4m+5����F��m+1��-��m+1��2-4��m+1��+5����M��m��3m+15����N��m+1��3��m+1��+15����
��ME��=-m2-4m+5-��3m+15��=-m2-7m-10��NF��=-m2-9m-18��
��ME��+NF��=-m2-7m-10-m2-9m-18=2m2-16m-28��
��-2��0��
��m=-$\frac{-16}{2����-2��}$=-4��
��ME��+NF�������ֵ����ʱE�䣨-4��5����F�䣨-3��8����
Ҫʹ|RE��-RF��|ֵ������E�䡢F�䡢R������һ��ֱ���ϣ�
����ֱ��E��F�䣺y=kx+b��k��0������
$\left\{\begin{array}{l}{-3k+b=8}\\{-4k+b=5}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=3}\\{b=17}\end{array}\right.$��
��ֱ��E��F�䣺y=3x+17��k��0����
��x=0ʱ��y=17�����R�������ǣ�0��17����
��ʱ��|RE��-RF��|�����ֵΪ$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$��
��3����ͼ2�����P��x��-x2-4x+5����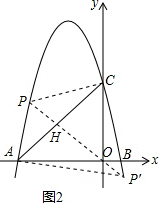
��PA=PCʱ����P���߶�AC�Ĵ�ֱƽ�����ϣ�
��OC=OA��
���O���߶�AC�Ĵ�ֱƽ�����ϣ�
���P�ڡ�AOC�Ľ�ƽ�����ϣ�
��-x=-x2-4x+5��
���x1=$\frac{-3+\sqrt{29}}{2}$��x2=$\frac{-3-\sqrt{29}}{2}$��
��P��$\frac{-3-\sqrt{29}}{2}$��$\frac{3+\sqrt{29}}{2}$����P�䣨$\frac{-3+\sqrt{29}}{2}$��$\frac{3-\sqrt{29}}{2}$����
��PH=OP-OH=$\frac{\sqrt{58}-2\sqrt{2}}{2}$��P��H=OP��+OH=$\frac{\sqrt{58}+2\sqrt{2}}{2}$��
��S��PAC=$\frac{1}{2}$AC•PH=$\frac{1}{2}$��5$\sqrt{2}$��$\frac{\sqrt{58}-2\sqrt{2}}{2}$=$\frac{5\sqrt{29}-10}{2}$��S��PAC=$\frac{1}{2}$AC•P��H=$\frac{1}{2}$��5$\sqrt{2}$��$\frac{\sqrt{58}+2\sqrt{2}}{2}$=$\frac{5\sqrt{29}+10}{2}$��
���� ���⿼���˶��κ����ۺ��⣮�����漰����֪ʶ���д���ϵ������һ�κ�������ʽ�����κ���ͼ���ϵ���������������κ�����ֵ�����Լ������ε�������㣮�����йض�������ʱҪע����������������۽����

 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�| A�� | ����ֵ���Ա�������������� | |
| B�� | ���㣨3-a��a��һֱ��ֱ��y=-x+3�� | |
| C�� | ֱ��y=-x+3��������Χ�ɵ��������ܳ���$3+3\sqrt{2}$ | |
| D�� | ֱ��y=-x+3�������������� |
| A�� | 36�� | B�� | 60�� | C�� | 72�� | D�� | 108�� |
 ��1����������ABC��ʹAB=AC=a����B=�Ϧ���������ͼ�ۼ�����д��������
��1����������ABC��ʹAB=AC=a����B=�Ϧ���������ͼ�ۼ�����д��������
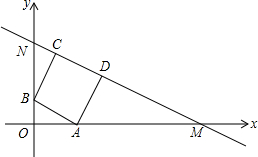 ��ֱ������ϵ�У�ֱ��MN�ֱ�x�ᡢy����������ڵ�N��M��������ABCD�ڽ���Rt��MON����A��B�ֱ����߶�MO��NO�ϣ���C��D���߶�MN�ϣ�����D������Ϊ��7��4�������C���꣨3��7����
��ֱ������ϵ�У�ֱ��MN�ֱ�x�ᡢy����������ڵ�N��M��������ABCD�ڽ���Rt��MON����A��B�ֱ����߶�MO��NO�ϣ���C��D���߶�MN�ϣ�����D������Ϊ��7��4�������C���꣨3��7����