题目内容
9. 如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=115°,则α=( )
如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=115°,则α=( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
分析 根据矩形的性质得∠B=∠D=∠BAD=90°,根据旋转的性质得∠D′=∠D=90°,∠4=α,利用对顶角相等得到∠1=∠2=115°,再根据四边形的内角和为360°可计算出∠3的度数,然后利用互余即可得到∠α的度数.
解答 解:如图,
∵四边形ABCD为矩形,
∴∠B=∠D=∠BAD=90°,
∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′,
∴∠D′=∠D=90°,∠4=α,
∵∠1=∠2=115°,
∴∠3=360°-90°-90°-115°=65°,
∴∠4=90°-65°=25°,
∴∠α=25°.
故答案为:25°.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了矩形的性质.

练习册系列答案
相关题目
20. 如图,点A在由函数y=(-1)2(x-3n)(x-3n-3)(3n≤x<3n+3,为自然数)的图象组成的平滑曲线上,点B在x轴上,且AB⊥x轴,若点B从原点O出发,沿x轴向右以每秒1个单位长的速度运动,则第2016秒时,点A的坐标是( )
如图,点A在由函数y=(-1)2(x-3n)(x-3n-3)(3n≤x<3n+3,为自然数)的图象组成的平滑曲线上,点B在x轴上,且AB⊥x轴,若点B从原点O出发,沿x轴向右以每秒1个单位长的速度运动,则第2016秒时,点A的坐标是( )
 如图,点A在由函数y=(-1)2(x-3n)(x-3n-3)(3n≤x<3n+3,为自然数)的图象组成的平滑曲线上,点B在x轴上,且AB⊥x轴,若点B从原点O出发,沿x轴向右以每秒1个单位长的速度运动,则第2016秒时,点A的坐标是( )
如图,点A在由函数y=(-1)2(x-3n)(x-3n-3)(3n≤x<3n+3,为自然数)的图象组成的平滑曲线上,点B在x轴上,且AB⊥x轴,若点B从原点O出发,沿x轴向右以每秒1个单位长的速度运动,则第2016秒时,点A的坐标是( )| A. | (2016,0) | B. | (2016,2) | C. | (2015,0) | D. | (2016,-2) |
4.顺次连接四边形ABCD各边的中点,所得四边形是( )
| A. | 平行四边形 | B. | 对角线互相垂直的四边形 | ||
| C. | 矩形 | D. | 菱形 |
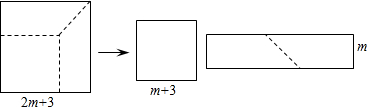
 某工厂接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该工厂招收了新工人,设新工人王浩第x天生产的粽子数量为y只,y与x满足如下关系:
某工厂接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该工厂招收了新工人,设新工人王浩第x天生产的粽子数量为y只,y与x满足如下关系: (1)求作:△ABC,使AB=AC=a,∠B=∠α(保留作图痕迹,不写作法);
(1)求作:△ABC,使AB=AC=a,∠B=∠α(保留作图痕迹,不写作法);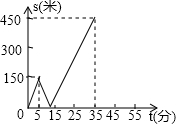 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示.
甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示.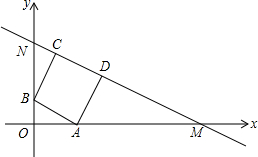 在直角坐标系中,直线MN分别交x轴、y轴的正半轴于点N、M,正方形ABCD内接于Rt△MON,点A、B分别在线段MO、NO上,点C、D在线段MN上.若点D的坐标为(7,4),则点C坐标(3,7).
在直角坐标系中,直线MN分别交x轴、y轴的正半轴于点N、M,正方形ABCD内接于Rt△MON,点A、B分别在线段MO、NO上,点C、D在线段MN上.若点D的坐标为(7,4),则点C坐标(3,7).