��Ŀ����
�Ķ�����Ľ����̣���y2��4y��8����Сֵ��
��������
y2��4y��8��y2��4y��4��4��(y+2)2+4��4����(y��2)2��0��(y��2)2����СֵΪ0����y2��4y��8����СֵΪ4.
��������Ľ����̣���m2��m��4����Сֵ��4��x2��2x�����ֵ.
m2+m+4����Сֵ�ǣ����ֵ��5. ����������������1������ʽ�䷽������ȫƽ��ʽ����ڵ���0�����������Сֵ����2������ʽ�䷽������ȫƽ��ʽ����ڵ���0������������ֵ�� ��������� �������� ��1��m2+m+4=(m+)2+���ߣ�m+��2��0�� ��(m+)2+�ݣ���m2+m+4����Сֵ�ǣ� ���ߡ�0�����5�������ֵ��5.
��ϰ��ϵ�д�
�����Ŀ


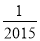 |���෴���ǣ�������
|���෴���ǣ�������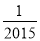 D. ��
D. ��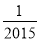
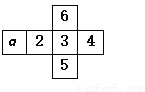
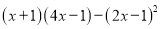
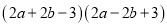
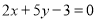 ����
����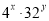 ��ֵ.
��ֵ.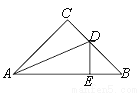
 ��EAB=��C,
��EAB=��C, ��CAE=��EAB=��C,
��CAE=��EAB=��C,
 ��C+��CAB=90�㣬
��C+��CAB=90�㣬 3��C=90�㣬
3��C=90�㣬 ��C=30��.
��C=30��.