题目内容
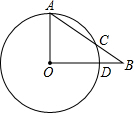如图，在Rt△AOB中，∠AOB=90°，以OA为半径的圆交AB于点C．若AO=5，OB=12，求BC的长．考点：垂径定理,勾股定理
专题：
分析：首先过点E作OE⊥AC于点E，利用三角形面积进而得出EO的长，即可得出AE以及AC的长，即可得出BC的长．
解答：
解：过点E作OE⊥AC于点E，
∵∠AOB=90°，AO=5，OB=12，
∴AB=13，
∴EO×AB=AO×BO，
∴EO=
=
=
，
在Rt△AEO中
AE=
=
，
∴AC=
×2=
，
∴BC=13-
=
．
解：过点E作OE⊥AC于点E，∵∠AOB=90°，AO=5，OB=12，
∴AB=13，
∴EO×AB=AO×BO，
∴EO=
| AO×BO |
| AB |
| 5×12 |
| 13 |
| 60 |
| 13 |
在Rt△AEO中
AE=
| AO2-EO2 |
| 25 |
| 13 |
∴AC=
| 25 |
| 13 |
| 50 |
| 13 |
∴BC=13-
| 50 |
| 13 |
| 119 |
| 13 |
点评：此题主要考查了勾股定理以及三角形面积应用和垂径定理等知识，得出EO的长是解题关键．
练习册系列答案
相关题目
两年前日本近海发生9.0级强震．该次地震导致地球当天自转快了0.0000016秒．这里的0.0000016用科学记数法表示为（ ）
| A、16×10-5 |
| B、1.6×10-5 |
| C、1.6×10-6 |
| D、1.6×10-6 |
如图，等边△ABC的边长为8，E是中线AD上一点，以CE为一边在CE下方作等边△CEF，连接BF并延长至点N，M为BN上一点，且CM=CN=5，则MN的长为
当a=1，b=2，c=3时，代数式c-（c-a）（c-b）=（ ）
| A、1 | B、2 | C、0 | D、以上均不对 |