题目内容
1.(1)计算:$\sqrt{12}$+($\frac{1}{2}$)-2-4sin60°;(2)先化简再求值:($\frac{2m}{m-1}$+$\frac{m}{1-m}$)÷m,其中m=$\sqrt{3}$+1.
分析 (1)根据负整数指数幂的意义,以及特殊角的锐角三角函数值即可求出答案.
(2)先化简原式,然后将m的值代入即可求出答案.
解答 解:(1)原式=2$\sqrt{3}$+4-4×$\frac{\sqrt{3}}{2}$=4
(2)当m=$\sqrt{3}$+1时,
原式=($\frac{2m}{m-1}$-$\frac{m}{m-1}$)×$\frac{1}{m}$
=$\frac{m}{m-1}$×$\frac{1}{m}$
=$\frac{1}{m-1}$
=$\frac{\sqrt{3}}{3}$
点评 本题考查学生的计算能力,解题的关键是熟练运用运算法则,本题属于基础题型.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
16.下列计算正确的是( )
| A. | a6÷a3=a2 | B. | (ab3)3=ab6 | C. | (a+2)2=a2+4 | D. | x12÷x6=x6 |
6.化简x6÷x2的结果是( )
| A. | x8 | B. | x4 | C. | x3 | D. | x |
10.计算(-x2n+1)3的结果正确的是( )
| A. | -x2n+4 | B. | -3x2n+1 | C. | -x6n+3 | D. | -x2n+3 |
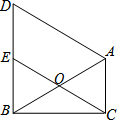 如图,在△ABC中,∠ACB=90°,∠ABC=30°.O为AB的中点,连接CO并延长到E,使OE=OC.过点A作AD∥CE交BE的延长线于D.
如图,在△ABC中,∠ACB=90°,∠ABC=30°.O为AB的中点,连接CO并延长到E,使OE=OC.过点A作AD∥CE交BE的延长线于D.
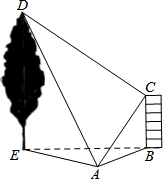 如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,求树高DE的长度.
如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,求树高DE的长度.