题目内容
11.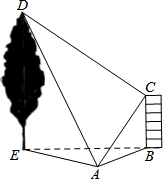 如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,求树高DE的长度.
如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,求树高DE的长度.
分析 首先解直角三角形求得表示出AC,AD的长,进而利用直角三角函数,求出答案.
解答  解:如图,在Rt△ABC中,∠CAB=45°,BC=6m,
解:如图,在Rt△ABC中,∠CAB=45°,BC=6m,
∴$AC=\frac{BC}{sin∠CAB}=6\sqrt{2}$(m);
在Rt△ACD中,∠CAD=60°,
∴$AD=\frac{AC}{cos∠CAD}=12\sqrt{2}$(m);
在Rt△DEA中,∠EAD=60°,$DE=AD•sin60°=12\sqrt{2}•\frac{{\sqrt{3}}}{2}=6\sqrt{6}(m)$,
答:树DE的高为$6\sqrt{6}$米.
点评 此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.

练习册系列答案
相关题目
2.下列实数中的无理数是( )
| A. | π | B. | $\frac{1}{2}$ | C. | 0.7 | D. | -8 |
3.某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共140件,进行手绘设计后了出售,所获利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如下表:
假设文化衫全部售出,共获利1860元,求黑白两种文化衫各多少件?
| 批发价(元) | 零售价(元) | |
| 黑色文化衫 | 10 | 25 |
| 白色文化衫 | 8 | 20 |
