题目内容
如图是一个几何体的三视图，这个几何体是考点：圆锥的计算,由三视图判断几何体
专题：计算题
分析：俯视图为圆的有圆锥，圆柱，球，根据主视图和左视图都是三角形可得到此几何体为圆锥，根据圆锥侧面积=底面周长×母线长÷2，可求得结果．
解答：解：此几何体为圆锥；
∵底面圆的半径为：r=1，圆锥高为：h=
，
∴圆锥母线长为：l=2，
∴侧面积=πrl=2π；
故答案为：圆锥，2π．
∵底面圆的半径为：r=1，圆锥高为：h=
| 3 |
∴圆锥母线长为：l=2，
∴侧面积=πrl=2π；
故答案为：圆锥，2π．
点评：本题考查了圆锥的计算，该三视图中的数据确定圆锥的底面直径和高是解本题的关键；本题体现了数形结合的数学思想，注意圆锥的高，母线长，底面半径组成直角三角形．
练习册系列答案
相关题目
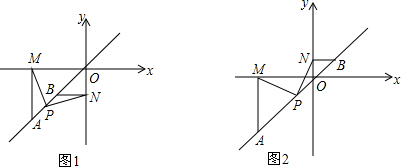
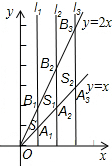如图，直线l1⊥x轴于点（1，0），直线l2⊥x轴于点（2，0），直线l3⊥x轴于点（3，0），…直线ln⊥x轴于点（n，0）．函数y=x的图象与直线l1，l2，l3…ln分别交于点A1，A2，A3，…An；函数y=2x的图象与直线l1，l2，l3…ln分别交于点B1，B2，B3…Bn，如果△OA1B1的面积记作S1，四边形A1A2B2B1的面积记作S2，四边形A2A3B3B2的面积记作S3…四边形An-1AnBnBn-1的面积记作Sn，那么S2014=若A（-1，y1），B（-3，y2）两点都在反比例函数y=
的图象上，则（ ）
| 3 |
| x |
| A、y1＞y2 |
| B、y1＜y2 |
| C、y1≤y2 |
| D、y1≥y2 |
已知a=
+
，b=
-
，则
的值为（ ）
| 3 |
| 2 |
| 3 |
| 2 |
| a2-ab+b2 |
| A、1 | B、2 | C、3 | D、4 |