题目内容
5．
如图，D在△ABC中BC边上，∠1=∠2，∠3=∠4．若∠BAC=75°，求∠DAC的度数．
分析 先根据三角形外角性质，得出∠3=∠4=∠1+∠2=2∠1，再根据三角形内角和定理，得出∠DAC+∠3+∠4=180°，最后根据∠DAC+4∠1=180°，以及∠BAC=∠1+∠DAC=75°，求得∠DAC的度数即可．
解答 解：∵∠1=∠2，∠3=∠4，
而∠4=∠1+∠2，
∴∠3=∠4=∠1+∠2=2∠1，
在△ADC中，∠DAC+∠3+∠4=180°，
∴∠DAC+4∠1=180°①，
∵∠BAC=∠1+∠DAC=75°②，
∴②×4-①得：∠DAC=40°．
点评 本题主要考查了三角形内角和定理以及三角形外角性质的综合应用，解题时注意：三角形的一个外角等于和它不相邻的两个内角的和．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
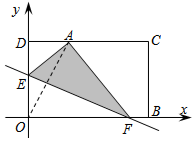如图，在平面直角坐标系中，一张矩形纸片OBCD按图所示放置，已知OB=10，BC=6，将这张纸片折叠，使点O落在CD上，记作点A，折痕与边OD交于点E，与边OB交于点F，已知点E的坐标为（0，4），则点A的坐标为（2$\sqrt{3}$，6）．
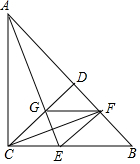如图．在Rr△ABC中，∠ACB=90°，CD⊥AB于D，∠BAC的平分线交CD于G，交BC于E，∠DCB的平分线交BD于F，连接EF，FG．
如图，在△ABC中，∠C=90°，∠BAC=60°，∠BAC的平分线交BC于D，若AD=6cm，则BC=9 cm．
17．【分校】下面三个有理数$-\frac{3}{4}$，$-\frac{5}{6}$，$-\frac{7}{8}$的大小顺序是（ ）
| A． | $-\frac{7}{8}$$＜-\frac{5}{6}$$＜-\frac{3}{4}$ | B． | $-\frac{7}{8}$$＜-\frac{3}{4}$$＜-\frac{5}{6}$ | C． | $-\frac{5}{6}$$＜-\frac{7}{8}$$＜-\frac{3}{4}$ | D． | $-\frac{3}{4}$$＜-\frac{5}{6}$$＜-\frac{7}{8}$ |
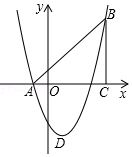如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90，AC=BC，OA=1，OC=4，抛物线y=x2+bx+c经过A，B两点，抛物线的顶点为D．