Question

11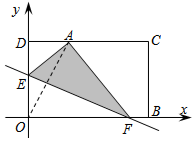．如图，在平面直角坐标系中，一张矩形纸片OBCD按图所示放置，已知OB=10，BC=6，将这张纸片折叠，使点O落在CD上，记作点A，折痕与边OD交于点E，与边OB交于点F，已知点E的坐标为（0，4），则点A的坐标为（2$\sqrt{3}$，6）．

Answer 1

分析 根据折叠的性质求出AE，根据勾股定理求出AD，根据矩形的性质得到答案．

解答 解：∵点E的坐标为（0，4），
∴OE=4，
则DE=OD-OE=2，
由折叠的性质可知，AE=OE=4，
由勾股定理得，AD=$\sqrt{A{E}^{2}-D{E}^{2}}$=2$\sqrt{3}$，
∴点A的坐标为（2$\sqrt{3}$，6），
故答案为：（2$\sqrt{3}$，6）．

点评 本题考查的是翻转变换的性质，掌握翻转变换是一种对称变换，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．