题目内容
8.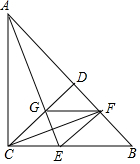 如图.在Rr△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线交CD于G,交BC于E,∠DCB的平分线交BD于F,连接EF,FG.
如图.在Rr△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线交CD于G,交BC于E,∠DCB的平分线交BD于F,连接EF,FG.(1)求证:四边形CEFG为菱形;
(2)若∠B=45°,请直接写出图中所有等腰直角三角形.
分析 (1)根据四边相等的四边形是菱形,即可证明.
(2)等腰直角三角形有:△ABC,△ACD,△CDB,△GDF,△EFB.
解答 (1)证明:∵∠ACB=90°,CD⊥AB,
∴∠CAD+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠CAD=∠BCD,同理∠ACD=∠B,
∵∠CAE=∠EAB,∠BCF=∠FCD,
∴∠BCF=∠CAE,
∵∠BCF+∠ACF=90°,
∴∠CAE+∠ACF=90°,
∴AE⊥CF,
∴∠CAE+∠ACF=90°,∠EAF+∠AFC=90°,
∴∠ACF=∠AFC,
∴AC=AF,
在△ACG和△AFG中,
$\left\{\begin{array}{l}{AG=AG}\\{∠GAC=∠GAF}\\{AC=AF}\end{array}\right.$,
∴△AGC≌△AGF,
∴CG=GF,同理证明CE=EF,
∵∠CGE=∠ACG+∠CAG,∠CEG=∠EAB+∠B,
∴∠CGE=∠CEG,
∴CG=CE=FG=EF,
∴四边形CEFG是菱形.
(2)当∠B=45°时,图中等腰直角三角形有:△ABC,△ACD,△CDB,△GDF,△EFB.
点评 本题考查菱形的判定和性质、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,本题的证明方法比较多,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图是某座桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为( )
如图是某座桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为( )
 如图是某座桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为( )
如图是某座桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为( )| A. | 13m | B. | 15m | C. | 20 m | D. | 26m |
2. 如图,△ABC中,∠A=90°,∠C=75°,AC=6,DE垂直平分BC,则BE的值为( )
如图,△ABC中,∠A=90°,∠C=75°,AC=6,DE垂直平分BC,则BE的值为( )
 如图,△ABC中,∠A=90°,∠C=75°,AC=6,DE垂直平分BC,则BE的值为( )
如图,△ABC中,∠A=90°,∠C=75°,AC=6,DE垂直平分BC,则BE的值为( )| A. | 12 | B. | 6$\sqrt{3}$ | C. | 8 | D. | 9 |
 已知:如图,在△ABC中,AB=AC,点D是BC延长线上一点,点E是边AC上一点,如果∠EBC=∠D,BC=4,cos∠ABC=$\frac{1}{3}$.
已知:如图,在△ABC中,AB=AC,点D是BC延长线上一点,点E是边AC上一点,如果∠EBC=∠D,BC=4,cos∠ABC=$\frac{1}{3}$. 如图,D在△ABC中BC边上,∠1=∠2,∠3=∠4.若∠BAC=75°,求∠DAC的度数.
如图,D在△ABC中BC边上,∠1=∠2,∠3=∠4.若∠BAC=75°,求∠DAC的度数.