题目内容
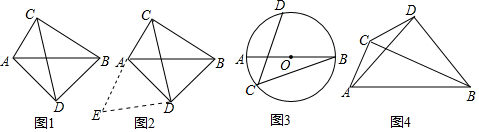
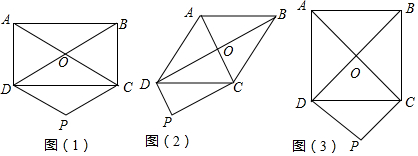
19.已知:?ABCD的对角线AC、BD相较于点O,过点D作DP∥OC且DP=OC,连接CP.得到四边形CODP.(1)如图(1),在?ABCD中,若∠ABC=90°,判断四边形CODP的形状,并证明;
(2)如图(2),在?ABCD中,若AB=AD,判断四边形CODP的形状,并证明;
(3)如图(3),在?ABCD中,若∠ABC=90°,且AB=AD,判断四边形CODP的形状,不需证明.
分析 (1)根据矩形的判定定理得到四边形ABCD是矩形,得到OD=OC,根据菱形的判定定理证明;
(2)根据菱形的判定定理得到四边形ABCD是菱形,得到∠DOC=90°,根据矩形的判定定理证明;
(3)根据正方形的判定定理得到四边形ABCD是正方形,得到∠DOC=90°,OD=OC,根据正方形的判定定理证明.
解答 解:(1)四边形CODP是菱形,
证明:∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
?ABCD中,∠ABC=90°,
∴四边形ABCD是矩形,
∴OD=OC,
∴四边形CODP是菱形;
(2)四边形CODP是矩形,
证明:?ABCD中,AB=AD,
∴四边形ABCD是菱形,
∴∠DOC=90°,
∴四边形CODP是矩形;
(3)四边形CODP是正方形,
证明:∵?ABCD中,∠ABC=90°,AB=AD,
∴四边形ABCD是正方形,
∴∠DOC=90°,OD=OC,
∴四边形CODP是正方形.
点评 本题考查的是矩形、菱形、正方形的性质和判定,掌握相关的性质定理和判定定理是解题的关键.

练习册系列答案
相关题目
9.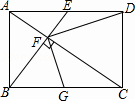 在矩形ABCD中,点E为AD的中点,连接BE,AC,AC⊥BE于点F,连接DF,下列结论.①CF=2AF;②△DEF与△DFA相似;③∠DFC=∠BAC;④当G是BC中点时,有FG=DE,其中正确的个数是( )
在矩形ABCD中,点E为AD的中点,连接BE,AC,AC⊥BE于点F,连接DF,下列结论.①CF=2AF;②△DEF与△DFA相似;③∠DFC=∠BAC;④当G是BC中点时,有FG=DE,其中正确的个数是( )
 在矩形ABCD中,点E为AD的中点,连接BE,AC,AC⊥BE于点F,连接DF,下列结论.①CF=2AF;②△DEF与△DFA相似;③∠DFC=∠BAC;④当G是BC中点时,有FG=DE,其中正确的个数是( )
在矩形ABCD中,点E为AD的中点,连接BE,AC,AC⊥BE于点F,连接DF,下列结论.①CF=2AF;②△DEF与△DFA相似;③∠DFC=∠BAC;④当G是BC中点时,有FG=DE,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14. 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长是( )
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长是( )
 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长是( )
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长是( )| A. | 14 | B. | 19 | C. | 18 | D. | 16 |
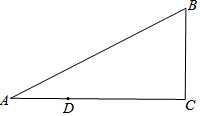 如图,已知△ABC,∠C=90°,点D在线段AC上,且CD=2AD.
如图,已知△ABC,∠C=90°,点D在线段AC上,且CD=2AD. 如图所示,点C在线段AB的延长线上,BC=$\frac{1}{3}$AB,D为AC中点,DC=4cm,求线段AB的长度.
如图所示,点C在线段AB的延长线上,BC=$\frac{1}{3}$AB,D为AC中点,DC=4cm,求线段AB的长度.