题目内容
9.关于x的一元二次方程x2+(2k+1)x+k2-1=0有两个不相等的实数根.(1)求k的取值范围;
(2)选择一个你喜欢的k值,并求此时方程的根.
分析 (1)根据方程的系数结合根的判别式,可得出△=4k+5>0,解之即可得出k的取值范围;
(2)选择k=1,将其代入原方程,利用分解因式法求出方程的解即可.
解答 解:(1)∵方程x2+(2k+1)x+k2-1=0有两个不相等的实数根,
∴△=(2k+1)2-4×1×(k2-1)=4k+5>0,
解得:k>-$\frac{5}{4}$.
(2)∵1>-$\frac{5}{4}$,
∴k值可以为1.
当k=1时,原方程为x2+3x=x(x+3)=0,
解得:x1=0,x2=-3.
点评 本题考查了根的判别式以及因式分解法解一元二次方程,解题的关键是:(1)根据方程的系数结合根的判别式,找出△=4k+5>0;(2)将k=1代入原方程,利用因式分解法解方程.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
4. 小米和小亮玩一种跳棋游戏,如图,游戏板由大小相等的小正方形组成,小米让棋子在游戏板上随意走动,则棋子落在白色区域的概率是( )
小米和小亮玩一种跳棋游戏,如图,游戏板由大小相等的小正方形组成,小米让棋子在游戏板上随意走动,则棋子落在白色区域的概率是( )
 小米和小亮玩一种跳棋游戏,如图,游戏板由大小相等的小正方形组成,小米让棋子在游戏板上随意走动,则棋子落在白色区域的概率是( )
小米和小亮玩一种跳棋游戏,如图,游戏板由大小相等的小正方形组成,小米让棋子在游戏板上随意走动,则棋子落在白色区域的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{9}{16}$ |
1.在“3.15”植树节活动后,对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分:

请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵;
(2)图1中,甲30%、乙20%,并将图2补充完整;
(3)若经观测计算得出丙种树苗的成活率为89.6%,求这次植树活动的树苗成活率.
| 栽下的各品种树苗棵数统计表 | ||||
| 植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
| 植树棵数 | 150 | 125 | 125 | |

请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵;
(2)图1中,甲30%、乙20%,并将图2补充完整;
(3)若经观测计算得出丙种树苗的成活率为89.6%,求这次植树活动的树苗成活率.
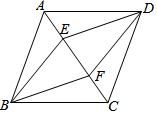 如图,在菱形ABCD中,点E、F在对角线AC上,且AE=CF.
如图,在菱形ABCD中,点E、F在对角线AC上,且AE=CF.