题目内容
9.某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件,第二个月如果单价不变,预计仍可以售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降1元,可多售出10件,但最低单价应高于购进的价格;第二月结束后.批发商核对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.(1)填表(不需化简)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量 | 200 | 200+10x | 800-200-(200+10x) |
(3)如果批发商希望通过销售这批T恤获利最大,那么第二个月的单价应是多少元?最大利润为多少?
分析 (1)根据题意直接用含x的代数式表示即可;
(2)利用“获利8000元”,即销售额-进价=利润,作为相等关系列方程,解方程求解后要代入实际问题中检验是否符合题意,进行值的取舍;
(3)建立二次函数,将二次函数的解析式配方后即可确定最值.
解答 解:(1)填表如下:(用含x的代数式表示)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(件) | 200 | 200+10x | 800-200-(200+10x) |
(2)根据题意,得
(80-50)×200+(80-50-x)(200+10x)-(50-40)(800-200-200-10x)=8000
整理,得x2-20x=0,
解这个方程得x1=15,x2=0.
x2=0不合题意舍弃
答:第二个月的单价应是65元.
(3)获得的利润y=(80-50)×200+(80-x-50)(200+10x)-(50-40)(800-200-200-10x)=-10(x-10)2+9000,
当第二个月单价降低10元,即单价是80-10=70元时,获得的最大利润是9000元.
点评 考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.有关销售问题中的等量关系一般为:利润=售价-进价,属于中考常考题型.

练习册系列答案
相关题目
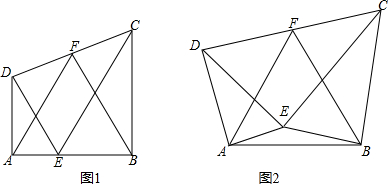
 如图,在四边形ABCD中,AB=3cm,CD=2cm,∠BAD=60°,∠CDA=∠CBA=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=3cm,CD=2cm,∠BAD=60°,∠CDA=∠CBA=90°,求四边形ABCD的面积.