题目内容
7.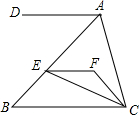 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=105°,∠ACF=25°.求∠FEC的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=105°,∠ACF=25°.求∠FEC的度数.
分析 先根据EF∥AD,AD∥BC得出EF∥AD∥BC,故∠DAC+∠ACB=180°.所以可得出∠BCF的度数,根据CE平分∠BCF可得出∠FCE=∠BCE,再由平行线的性质即可得出结论.
解答 解:∵EF∥AD,AD∥BC,
∴EF∥AD∥BC,
∴∠DAC+∠ACB=180°.
∵∠DAC=105°,∠ACF=25°,
∴∠BCF=180°-∠DAC-∠ACF=180°-105°-25°=50°.
∵CE平分∠BCF,
∴∠FCE=∠BCE=25°.
∵EF∥BC,
∴∠FEC=∠BCE=25°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
相关题目
15.立方根等于它本身的所有数为( )
| A. | -1,0,1 | B. | 0,1 | C. | 0,-1 | D. | 1 |
12.下列各式能用平方差公式计算的是( )
| A. | (2a+b)(2b-a) | B. | (-a+b)(a-b) | C. | (a+b)(a-2b) | D. | (a+b)(b-a) |
19.下列命题中的假命题是( )
| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 对顶角相等,两直线平行 |
16.若(x+k)2=x2+2kx+9,则k的值是( )
| A. | 3或-3 | B. | 6或-6 | C. | 9或-9 | D. | 1或-1 |
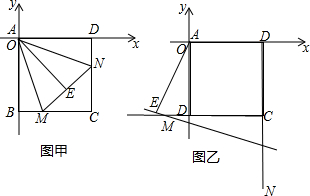
 如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE. 如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=35°,则∠2=125°.
如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=35°,则∠2=125°.