题目内容
17.如图,已知直线AB:y=-$\frac{1}{2}$x+3,直线AC:y=x-3,点P是直线AB上的动点,过点P作PQ∥y轴交直线AC于点Q,过点P,Q分别作PM⊥y轴于点M,QN⊥y轴于点N,设点P的横坐标为m,当矩形PMNQ的周长为10时,m=2.
分析 由点P的横坐标及直线AB、AC解析式表示出点P、Q的坐标,再根据矩形PMNQ的周长列出关于m的绝对值方程,解方程可得m的值.
解答 解:根据题意,点P的坐标为(m,$\frac{1}{2}$m-3),点Q的坐标为(m,m-3),
∵矩形PMNQ的周长为10,
∴2|m|+2|-$\frac{1}{2}$m+3-m+3|=10,即|m|+|-$\frac{3}{2}$m+6|=5,
当m≤0时,-m+$\frac{3}{2}$m-6=0,
解得:m=22(舍);
当0<m<4时,m+$\frac{3}{2}$m-6=5,
解得:m=$\frac{22}{5}$(舍);
当m≥4时,m-$\frac{3}{2}$m+6=5,
解得:m=2;
故答案为:2.
点评 本题主要考查一次函数图象上点的坐标及两点间的距离公式、解绝对值方程,根据题意列出关于m的绝对值方程并求解是解题的关键.

练习册系列答案
相关题目
7. 如图,边长为1的小正方形构成的网格中,⊙O半径为1,圆心O在格点上,则tan∠AED=( )
如图,边长为1的小正方形构成的网格中,⊙O半径为1,圆心O在格点上,则tan∠AED=( )
 如图,边长为1的小正方形构成的网格中,⊙O半径为1,圆心O在格点上,则tan∠AED=( )
如图,边长为1的小正方形构成的网格中,⊙O半径为1,圆心O在格点上,则tan∠AED=( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
8.-$\frac{3}{4}$是下列各算式中( )的积.
| A. | -3$\frac{1}{2}$×(-$\frac{3}{14}$) | B. | $\frac{3}{4}$×(-$\frac{5}{6}$) | C. | (-1$\frac{1}{2}$)×$\frac{4}{9}$ | D. | $\frac{4}{5}$×(-$\frac{15}{16}$) |
5.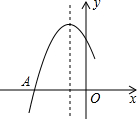 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
①b2>4ac;
②2a+b=0;
③a+b+c>0;
④若B(-5,y1)、C(-1,y2 )为函数图象上的两点,则y1<y2.
其中正确结论是( )
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:①b2>4ac;
②2a+b=0;
③a+b+c>0;
④若B(-5,y1)、C(-1,y2 )为函数图象上的两点,则y1<y2.
其中正确结论是( )
| A. | ②④ | B. | ①③④ | C. | ①④ | D. | ②③ |
2. 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∠ABC+∠ADC=120°,则∠A的度数是( )
如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∠ABC+∠ADC=120°,则∠A的度数是( )
 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∠ABC+∠ADC=120°,则∠A的度数是( )
如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∠ABC+∠ADC=120°,则∠A的度数是( )| A. | 100° | B. | 110° | C. | 120° | D. | 125° |