题目内容
3.先化简,再求值:($\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$)÷$\frac{x+2}{{{x^2}-2x+1}}$,请你从-1、+1、-2、+2中选出你认为合理的x的值代入化简后的式子中求值x.分析 先化简题目中的式子,然后选取一个使得原分式有意义的x的值代入即可解答本题.
解答 解:($\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$)÷$\frac{x+2}{{{x^2}-2x+1}}$
=[$\frac{3x+4}{(x+1)(x-1)}-\frac{2(x+1)}{(x+1)(x-1)}$]÷$\frac{x+2}{{{x^2}-2x+1}}$
=$\frac{x+2}{(x+1)(x-1)}•\frac{{{{(x-1)}^2}}}{x+2}$
=$\frac{x-1}{x+1}$,
当x=2时,原式=$\frac{2-1}{2+1}=\frac{1}{3}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法,注意x≠±1,-2.

练习册系列答案
相关题目
13.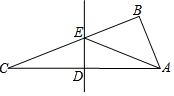 如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
 如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
14.已知a,b互为相反数,c,d互为倒数,x的绝对值是2,计算x2-cd•x+(a+b)2017=( )
| A. | 2或-2 | B. | 2或6 | C. | 2 | D. | 3 |
18.下列四个图形中,线段BE是△ABC的高的是( )
| A. | 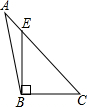 | B. | 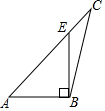 | C. | 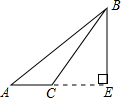 | D. | 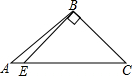 |
12.某水果公司把一批水果运到外地,现有汽车和火车两种运输方式可供选择,运输过程中的损耗均为100元/时.其它主要参考数据如下:
(1)请分别写出汽车、火车运输的总费用y(元)与运输路程x(千米)之间的关系式;(提示:总费用=运输费+损耗费+袋卸费)
(2)当运输路程x(千米)为多少时,汽车、火车两种运输方式的总费用相同.
| 运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费(元) |
| 汽车 | 50 | 20 | 900 |
| 火车 | 100 | 15 | 2000 |
(2)当运输路程x(千米)为多少时,汽车、火车两种运输方式的总费用相同.
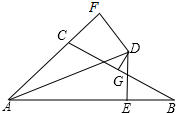 如图∠BAC的平分线AD与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=22,AC=10,则BE=6.
如图∠BAC的平分线AD与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=22,AC=10,则BE=6. 如图,已知A、B、C、D四点在同一直线上,点D是线段BC的中点,且BC=3AB,如果AB=4cm,则线段AD的长度为10cm.
如图,已知A、B、C、D四点在同一直线上,点D是线段BC的中点,且BC=3AB,如果AB=4cm,则线段AD的长度为10cm.