题目内容
17.(1)解分式方程:$\frac{1}{x-3}$=3+$\frac{x}{3-x}$(2)解不等式组:$\left\{\begin{array}{l}{x-3(x-2)≤8}\\{x-4<\frac{x+1}{3}}\end{array}\right.$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)去分母得:1=3x-9-x,
解得:x=5,
经检验x=5是分式方程的解;
(2)$\left\{\begin{array}{l}{x-3(x-2)≤8①}\\{x-4<\frac{x+1}{3}②}\end{array}\right.$,
由①得:x≥-1,
由②得:x<$\frac{13}{2}$,
则不等式组的解集为-1≤x<$\frac{13}{2}$.
点评 此题考查了解分式方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
6.已知甲、乙两种商品的进价和为100元,为了促销而打折销售,若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元,甲、乙两种商品的定价分别为( )
| A. | 50元、150元 | B. | 50元、100元 | C. | 100元、50元 | D. | 150元、50元 |
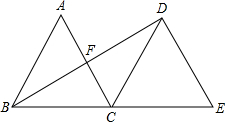 如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.求线段BD的长.
如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.求线段BD的长.