题目内容
5.先化简,再求值:($\frac{x}{{x}^{2}+2x}$-1)÷$\frac{x+1}{{x}^{2}-4}$,其中x是方程$\frac{2}{x-3}$=$\frac{3}{x}$的解.分析 先将($\frac{x}{{x}^{2}+2x}$-1)÷$\frac{x+1}{{x}^{2}-4}$进行化简,然后根据x是方程$\frac{2}{x-3}$=$\frac{3}{x}$的解求出x的值,并将x的值代入求解即可.
解答 解:原式=$\frac{x-({x}^{2}+2x)}{x(x+2)}$÷$\frac{x+1}{(x-2)(x+2)}$
=$\frac{-{x}^{2}-x}{x(x+2)}$×$\frac{(x+2)(x-2)}{x+1}$
=$\frac{-x(x+1)}{x(x+2)}$×$\frac{(x+2)(x-2)}{x+1}$
=2-x.
∵x是方程$\frac{2}{x-3}$=$\frac{3}{x}$的解,
∴解方程$\frac{2}{x-3}$=$\frac{3}{x}$,得x=9,
经检验,x=9是原方程的解.
∴当x=9时,原式=2-9=-7.
点评 本题考查了分式的化简求值,解答本题的关键在于先将($\frac{x}{{x}^{2}+2x}$-1)÷$\frac{x+1}{{x}^{2}-4}$进行化简,然后根据x是方程$\frac{2}{x-3}$=$\frac{3}{x}$的解求出x的值,并将x的值代入求解.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
20.旅行社组织了甲、乙两个旅游团到游乐场游玩,两团总报名人数为120人,其中甲团人数不超过50人,游乐场规定一次性购票50人以上可享受团队票.门票价格如下:
旅行社经过计算后发现,如果甲、乙两团合并成一个团队购票可以比分开购票节约300元.
(1)求甲、乙两团的报名人数;
(2)当天到达游乐场后发现团队票价格作了临时调整,团队票A每张降价a元,团队票B每张降价2a元,同时乙团队因故缺席了30人,此时甲、乙两团合并成一个团队购票可以比分开购票节约225元,求a的值.
| 门票类别 | 散客票 | 团队票A | 团队票B |
| 购票要求 | 超过50人但不超过100人 | 超过100人 | |
| 票价(元/人) | 80元/人 | 70元/人 | 60元/人 |
(1)求甲、乙两团的报名人数;
(2)当天到达游乐场后发现团队票价格作了临时调整,团队票A每张降价a元,团队票B每张降价2a元,同时乙团队因故缺席了30人,此时甲、乙两团合并成一个团队购票可以比分开购票节约225元,求a的值.
 按照如图的程序计算,若输入n的值为3时,计算结果为231.
按照如图的程序计算,若输入n的值为3时,计算结果为231.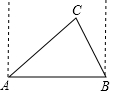 某次军事演习中,有三艘军舰在同一时刻向指挥所报告:A军舰说B军舰在它的正东方向,C军舰在它的北偏东60°方向;B军舰说C军舰在它的北偏西30°方向,C军舰说它到B军舰的距离比它到A军舰的距离近30海里,求A,B军舰的距离?(结果精确到0.1海里,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某次军事演习中,有三艘军舰在同一时刻向指挥所报告:A军舰说B军舰在它的正东方向,C军舰在它的北偏东60°方向;B军舰说C军舰在它的北偏西30°方向,C军舰说它到B军舰的距离比它到A军舰的距离近30海里,求A,B军舰的距离?(结果精确到0.1海里,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.
如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y. 如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.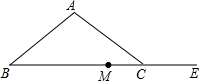 如图,在△ABC中,AB=AC.
如图,在△ABC中,AB=AC.