题目内容
13.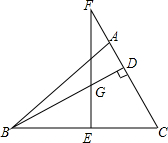 已知:如图,△ABC中,BD⊥AC,D为垂足,BC的垂直平分线EF分别交BD,CA的延长线于点G、F,E为垂足,且DF=$\frac{1}{2}$BC,求证:∠ACB=2∠F.
已知:如图,△ABC中,BD⊥AC,D为垂足,BC的垂直平分线EF分别交BD,CA的延长线于点G、F,E为垂足,且DF=$\frac{1}{2}$BC,求证:∠ACB=2∠F.
分析 连结CG,利用垂直平分线的性质得到BG=CG,BE=EC=$\frac{1}{2}$BC,从而得到∠GBE=∠GCB,DF=BE,证明△BEG≌△FDG(AAS),得到∠F=∠GBE,GE=GD,证明CG平分∠ACB,所以∠ACB=2∠GCB,即可得到∠ACB=2∠F.
解答 解:如图,连结CG,
∵BD⊥AC,EF垂直平分BC
∴BG=CG,BE=EC=$\frac{1}{2}$BC,
∴∠GBE=∠GCB,
∵DF=$\frac{1}{2}$BC,
∴DF=BE
在△BEG和△FDG中$\left\{\begin{array}{l}∠BGE=∠FGD\\∠BEG=∠FDG\\ BE=FD\end{array}\right.$
∴△BEG≌△FDG(AAS)
∴∠F=∠GBE,GE=GD,
而GE⊥BC,GD⊥AC
∴CG平分∠ACB,
∴∠ACB=2∠GCB,
∴∠ACB=2∠F.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明△BEG≌△FDG.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
8.若对于任意数x分式$\frac{x}{{{x^2}+m}}$都有意义,则m所满足的条件是( )
| A. | m≠0 | B. | m<0 | C. | m>0 | D. | m≥0 |
18.已知等腰三角形的腰长为9cm,则下列长度的四条线段中,能作为底边的是( )
| A. | 22cm | B. | 20cm | C. | 18cm | D. | 16cm |
5.如果x+3y=2003,那么[(x2+2xy-3y2)-4006(x-y)]÷(x-y)的值是( )
| A. | 2003 | B. | -2003 | C. | 4006 | D. | 不能确定 |
2.下列计算错误的是( )
| A. | x3m+1=(x3)m+1 | B. | x3m+1=x•x3m | C. | x3m+1=xm•x2m•x | D. | x3m+1=(xm)3•x |