题目内容
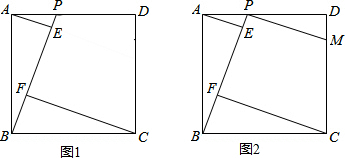
17．
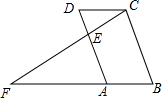如图，在平行四边形ABCD中，E是AD上一点，连接CE并延长交BA的延长线于点F，则下列结论中错误的是（ ）| A． | ∠AEF=∠DEC | B． | BC：DE=CF：CE | C． | FA：AB=FE：EC | D． | FA：CD=AD：DE |
分析 由平行四边形可得AD∥BC，AB∥CD，AB=CD，∠AEF与∠DEC是对顶角，再由平行线分线段成比例即可得出题中的线段是否成比例．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，AB=CD，AD=BC，
∴AD：DE=CF：CE，FA：CD=EF：EC，
即BC：DE=CF：CE，FA：AB=EF：EC，
∴FA：CD=AE：DE≠AD：DE，
又∠AEF与∠DEC是对顶角，所以∠AEF=∠DEC．
故选D．
点评 本题主要考查了平行四边形的性质以及平行线分线段成比例的性质，能够熟练掌握．
练习册系列答案
全能练考卷系列答案
相关题目
8．
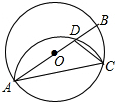如图，AB为⊙O的直径，点C为圆上一点，∠BAC=25°，若将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D，连结CD，则∠DCA的度数为（ ）
如图，AB为⊙O的直径，点C为圆上一点，∠BAC=25°，若将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D，连结CD，则∠DCA的度数为（ ）| A． | 35° | B． | 40° | C． | 45° | D． | 50° |
5．
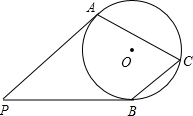如图，PA，PB是⊙O的切线，切点分别为A，B，点C在⊙O上，且$\widehat{ACB}$是优弧，则∠ACB等于（ ）
如图，PA，PB是⊙O的切线，切点分别为A，B，点C在⊙O上，且$\widehat{ACB}$是优弧，则∠ACB等于（ ）| A． | 180°-2∠P | B． | 180°-∠P | C． | 90°-$\frac{1}{2}$∠P | D． | ∠P |
12．下列运算中，计算结果正确的是（ ）
| A． | x3+x3=x6 | B． | （3a）2×（3a-2）=1 | C． | （-a）3•a2=-a6 | D． | （-4m2n）2=16m4n2 |
2．给定下列条件，不能判定△ABC是直角三角形的是（ ）
| A． | ∠A=∠B=2∠C | B． | ∠A+∠B=∠C | C． | ∠A：∠B：∠C=1：4：5 | D． | ∠A=37°，∠B=53° |
9．如果三角形的两边长分别为3和6，第三边长是奇数，则第三边长可以是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 9 |
6．为了解某市参加中考的45000名学生的身高情况，抽查了其中1500名学生的身高进行统计分析．下面叙述正确的是（ ）
| A． | 45000名学生是总体 | |
| B． | 1500名学生的身高是总体的一个样本 | |
| C． | 每名学生是总体的一个个体 | |
| D． | 以上调查是全面调查 |
