题目内容

8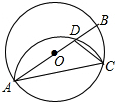．如图，AB为⊙O的直径，点C为圆上一点，∠BAC=25°，若将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D，连结CD，则∠DCA的度数为（　　）
A．35°B．40°C．45°D．50°

分析 连接OC，求出∠OCA=∠BAC=25°，求出∠AOC的度数，根据圆周角定理解答．

解答 解：连接OC，
∵OA=OC，
∴∠OCA=∠BAC=25°，
∴∠AOC=130°，即$\widehat{AC}$的度数是130°，
∵∠BAC=25°，
∴$\widehat{CD}$的度数是50°，
∴$\widehat{AD}$的度数是80°，
∴∠DCA=40°，
故选：B．

点评 本题考查的是圆周角定理的应用，掌握弧、圆心角的关系、圆周角定理是解题的关键．

练习册系列答案
相关题目
3．若代数式$\frac{1}{x-1}$在实数范围内有意义，则实数x的取值范围是（　　）
A．x＜1B．x＞1C．x≠1D．x=1
19．2$\frac{5}{6}$的倒数是$\frac{6}{17}$．
16．a，b为实数，a2+b2-3a-$\frac{1}{2}b+\frac{37}{16}$=0，a-4$\sqrt{b}$=-$\frac{1}{2}$．
3．计算：
①$\sqrt{4}+\sqrt{{{（-3）}^2}}$
②2$\sqrt{2}$-|1-2$\sqrt{2}$|
13．如图（1），抛物线W1：y=-x2+4x与x轴的正半轴交于点B，顶点为A，抛物线W2与W1关于x轴对称，顶点为D．
（1）求抛物线W2的解析式；
（2）将抛物线W2向右平移m个单位，点D的对应点为D′，点B的对应点为B′，则当m为何值时，四边形AOD′B′为矩形？请直接写出m的值．
（3）在（2）的条件下，将△AOD′沿x轴的正方向向右平移n个单位（0＜n＜5），得到△A′O′D′′，AD′分别与O′A′、O′D′′交于点M、点P，A′D′′分别与AB′、B′D′交于点N、点Q．
①求当n为何值时，四边形MNQP为菱形？
②若四边形MNQP的面积为S，求S关于n的函数关系式；并求当n为何值时，S的值最大？最大值为多少？
20．如图，已知点A的坐标为（-2，0），直线y=-x+4，与x轴，y轴分别交点B和点C，连接AC，顶点为D的抛物线y=ax2+bx+c过A，B，C三点．

（1）求抛物线的表达式；
（2）设抛物线的对称轴DE交线段BC于点E，P为第一象限内抛物线上的一点，过点P作x轴的垂线，交线段BC于点F，若四边形DEFP为平行四边形，求点P的坐标；
（3）设点M是线段BC上的一动点，过点M作MN∥AB，交AC于点N，点Q从点B出发以每秒1个单位长度的速度沿线段BA向点A运动，运动时间为t（秒）．
①若点Q满足75°＜∠BQC≤120°时，请直接写出运动时间t（秒）的范围4-$\frac{4}{3}$$\sqrt{3}$≤t＜12-4$\sqrt{3}$
②当t（秒）为何值时，△QMN为等腰直角三角形？
17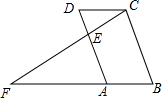．如图，在平行四边形ABCD中，E是AD上一点，连接CE并延长交BA的延长线于点F，则下列结论中错误的是（　　）
A．∠AEF=∠DECB．BC：DE=CF：CEC．FA：AB=FE：ECD．FA：CD=AD：DE
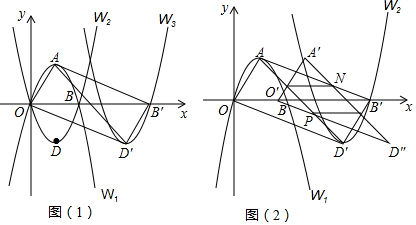
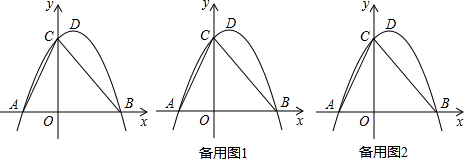
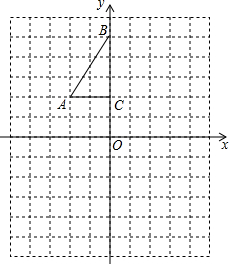18．如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点坐标分别为A（-2，2），B（0，5），C（0，2）．
（1）将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形；
（2）平移△ABC，使点A的对应点A2坐标为（-2，-6），请画出平移后对应的△A2B2C2的图形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网