Question

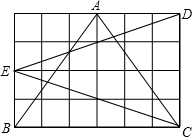如图是单位长度为1的网格，比较图中△ABC和△CDE的面积、周长的大小．

Answer 1

考点：勾股定理,三角形的面积

专题：网格型

分析：在网格中，利用勾股定理求出DE，CE，AB，AC的长，确定出DC与BC的长，即可确定出两三角形的周长与面积．

解答：解：根据勾股定理得：DE=EC=

22+62

=2

10

，AB=AC=

32+42

=5，
∵BC=6，DC=4，
∴△EDC的周长为4

10

+4；△ABC周长为5+5+6=16，
△EDC面积为

1

2

×4×6=12；△ABC面积为

1

2

×6×4=12．

点评：此题考查了勾股定理，以及三角形的面积，熟练掌握勾股定理是解本题的关键．