题目内容
已知α、β是方程x2-3x-5=0的两根,求
+
+β2的值.
| 25 |
| 2α-1 |
| 13 |
| α+2β |
考点:根与系数的关系
专题:
分析:先由一元二次方程的解的定义及根与系数的关系得出α=3-β,αβ=-5,β2=3β+5,将它们代入
+
+β2,化简即可求解.
| 25 |
| 2α-1 |
| 13 |
| α+2β |
解答:解:∵α、β是方程x2-3x-5=0的两根,
∴α+β=3,αβ=-5,β2-3β-5=0.
∴α=3-β,β2=3β+5,
∴
+
+β2
=
+
+3β+5
=
+
+3β+5
=
+3β+5
=
+3β+5
=
+5
=
+5
=7+5
=12.
∴α+β=3,αβ=-5,β2-3β-5=0.
∴α=3-β,β2=3β+5,
∴
| 25 |
| 2α-1 |
| 13 |
| α+2β |
=
| 25 |
| 2(3-β)-1 |
| 13 |
| 3-β+2β |
=
| 25 |
| 5-2β |
| 13 |
| 3+β |
=
| 25(3+β)+13(5-2β) |
| (5-2β)(3+β) |
=
| 140-β |
| 5-7β |
=
| 140-β+3β(5-7β) |
| 5-7β |
=
| 35-49β |
| 5-7β |
=7+5
=12.
点评:本题考查了根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.同时考查了一元二次方程的解的定义及分式的化简求值.
| b |
| a |
| c |
| a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点A,B,C在⊙O上,已知∠ABC=130°,则∠AOC=( )
如图,点A,B,C在⊙O上,已知∠ABC=130°,则∠AOC=( )| A、100° | B、110° |
| C、120° | D、130° |
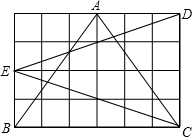 如图是单位长度为1的网格,比较图中△ABC和△CDE的面积、周长的大小.
如图是单位长度为1的网格,比较图中△ABC和△CDE的面积、周长的大小. 如图,AB∥x轴,分别交双曲线y=
如图,AB∥x轴,分别交双曲线y=