题目内容
从甲地到乙地的公路只有上坡路和下坡路,没有平路,一辆汽车上坡时每小时行驶20千米,下坡时每小时行驶35千米,车从甲地开往乙地需9小时,乙地开往甲地需7小时,问:甲、乙两地间路由多少千米?从甲地到乙地须行驶多少千米的上坡路?
考点:二元一次方程组的应用
专题:
分析:设从甲地到乙地的上坡路为x千米,下坡路为y千米,再根据上坡和下坡时的速度和从甲地开往乙地需的时间,从乙地到甲地需的时间,列出并解方程组即可.
解答:解:设从甲地到乙地的上坡路为x千米,下坡路为y千米,由题意得,
解这个方程组,得,
甲、乙两地间的公路的千米数:
+
=
(千米),
从甲地到乙地上坡路的千米数:
千米.
答:甲、乙两地间的公路有
千米;从甲地到乙地须行驶
千米的上坡路.
|
解这个方程组,得,
|
甲、乙两地间的公路的千米数:
| 4900 |
| 33 |
| 1820 |
| 33 |
| 2240 |
| 11 |
从甲地到乙地上坡路的千米数:
| 4900 |
| 33 |
答:甲、乙两地间的公路有
| 2240 |
| 11 |
| 4900 |
| 33 |
点评:此题考查用二元一次方程组解决实际问题,关键是根据题意找出等量关系式,列出并解方程组即可.

练习册系列答案
相关题目
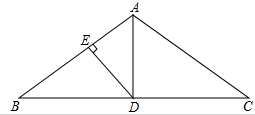 如图所示,在△ABC中,∠BAC=120°,AB=AC,AD是高,DE⊥AB于点E,且AE=2,求AB的长.
如图所示,在△ABC中,∠BAC=120°,AB=AC,AD是高,DE⊥AB于点E,且AE=2,求AB的长.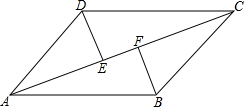 已知:如图,AB=CD,DE=BF,DE⊥AC,BF⊥AC.求证:AB∥CD.
已知:如图,AB=CD,DE=BF,DE⊥AC,BF⊥AC.求证:AB∥CD.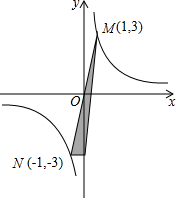 如图,求阴影部分的面积.
如图,求阴影部分的面积.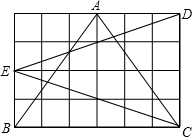 如图是单位长度为1的网格,比较图中△ABC和△CDE的面积、周长的大小.
如图是单位长度为1的网格,比较图中△ABC和△CDE的面积、周长的大小.